Written by TACEO
on October 31, 2024

The Surprising Efficiency of Honest-Majority MPC for coSNARKs

After our recent blog posts about a large-scale MPC use case together with Worldcoin and about coSNARKs, we wanted to take a closer look at some specific MPC protocols, investigate what makes them efficient for coSNARKs, and discuss some specific optimizations we recently found and implemented in our coSNARKs code base.

Honest-Majority MPC

Here we assume some knowledge of MPC, but if you'd like to get familiar with the basics, please look at the introduction in our previous blog or in books like Pragmatic MPC. To sum up with just one sentence: With MPC, multiple mutually untrusting parties can compute a function on their combined private inputs without leaking the inputs or intermediate results to each other.

MPC comes in lots of different flavors with different protocols and security settings. The setting which we are mostly interested in during this blog post is honest-majority. In this setting, the protocol is only considered to be secure as long as a majority of the involved parties behave honestly. This means, that only less than half of all parties are allowed to collude, and any more parties can reconstruct secrets. An opposing model would be dishonest-majority which is considered secure even if malicious parties outnumber honest ones---parties cannot reconstruct secrets if at least one party is not willing to collude. So why do we care about the arguably weaker setting of honest-majority? The reason for this is largely down to performance. But first let us clarify a common misconception about security models, namely that the models semi-honest and malicious security are additional properties to honest/dishonest majority protocol. We can have protocols that are secure against semi-honest adversaries with dishonest majority, as well as protocols secure against malicious parties with an honest majority. To summarize, semi-honest/malicious security defines how strong malicious parties are, honest/dishonest majority how many malicious parties can be handled by the protocol. 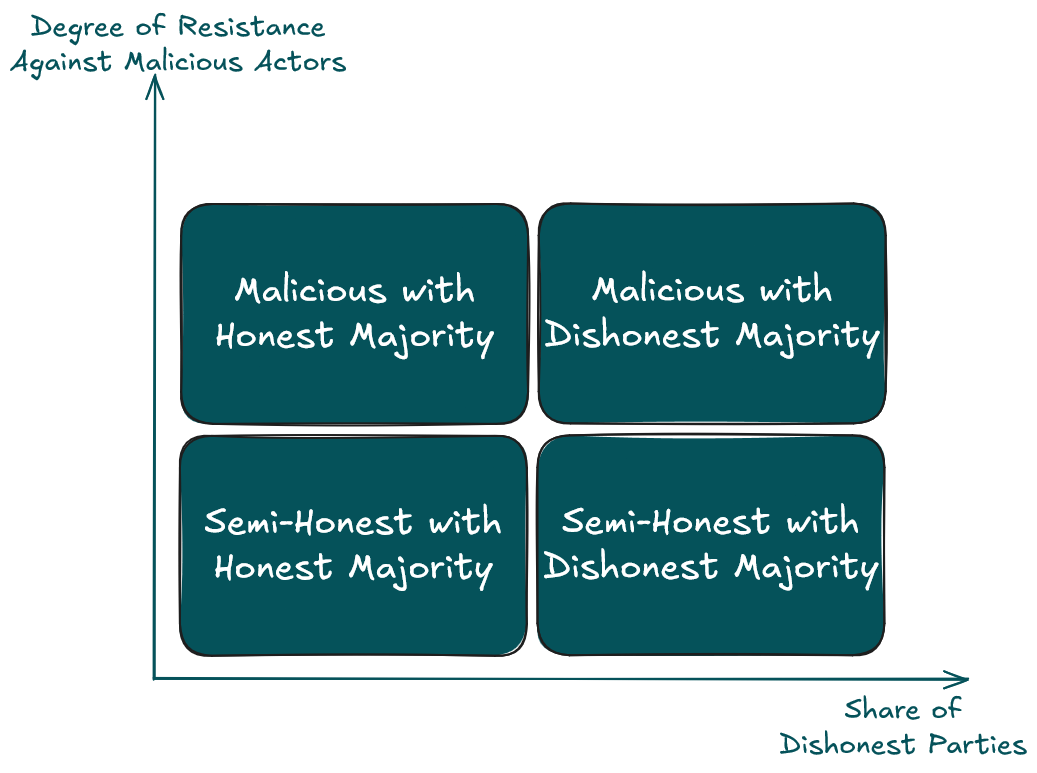See the following picture: Security of MPC protocols

Figure 1: The security models of MPC protocols.

The honest-majority protocols that we use in our implementation are either based on replicated sharing (see, e.g., ABY3) or Shamir secret sharing (see the original 2-page long paper from 1979, back when papers were still short and readable).

Shamir secret sharing is one of the fundamental building blocks of MPC and works by sharing values as points on polynomials. Let's demonstrate by sharing a value $a\in \mathbb F_p$ with $n$ parties: First, the party knowing $a$ creates a random degree-$d$ (more on the choice of $d$ later) polynomial with $a$ in the constant term: $$ p(X) = a + r_1 \cdot X + r_2 \cdot X^2 + \dots r_d \cdot X^d $$ Then, it will give each party a point on the polynomial: $$ \text{Party}~1: p(1) \newline \text{Party}~2: p(2) \newline \dots \newline \text{Party}~n: p(n) $$ So why do we do that? First, observe that for any degree-$d$ polynomial, it can be reconstructed by $d+1$ points (e.g., by Lagrange interpolation) while $\le d$ points give statistically no information about it. See also the illustration with degree-2 polynomials:

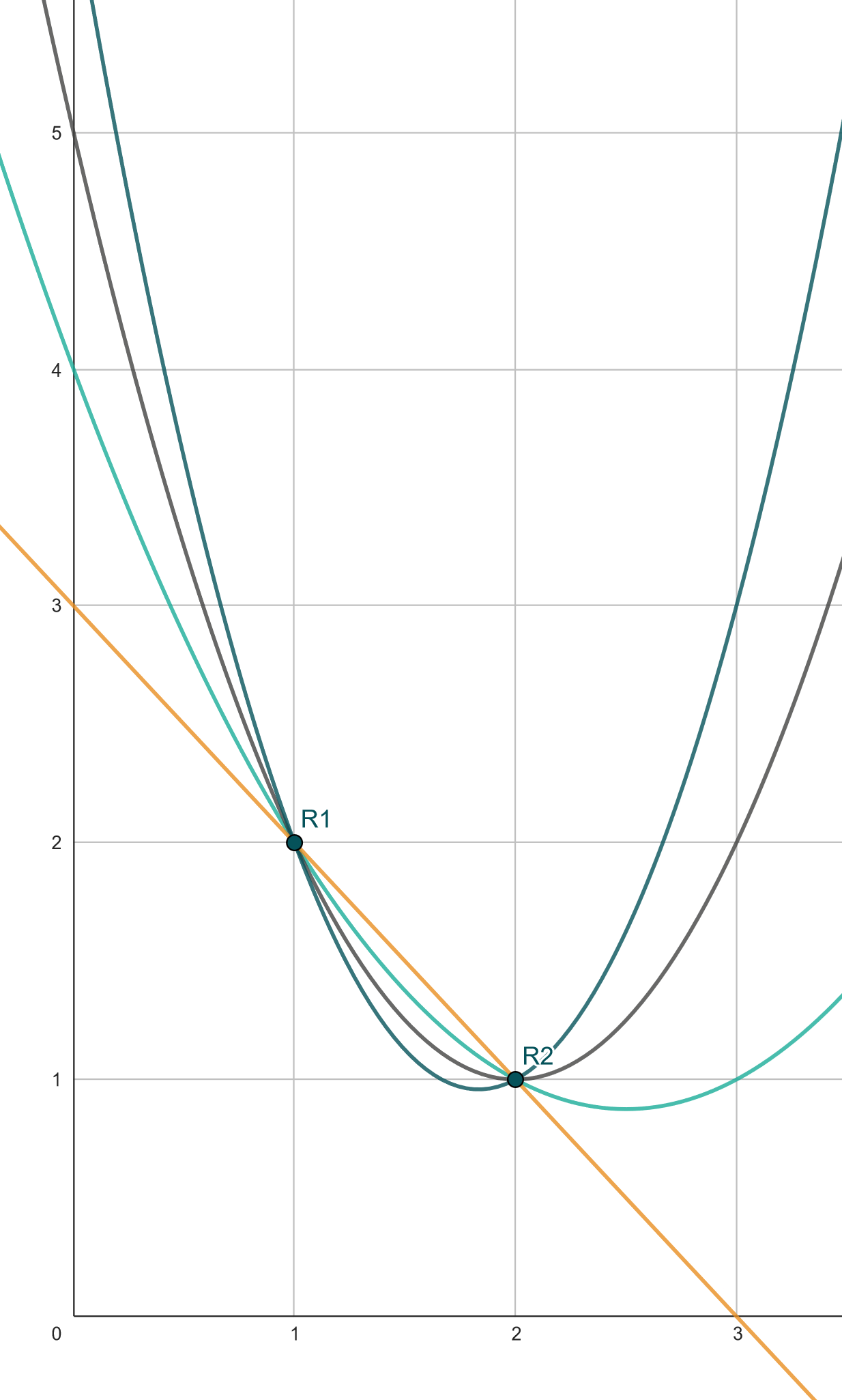
Figure 2: Interpolating a degree-2 polynomial with just 2 points gives $|\mathbb F_p|$ options over $\mathbb F_p$.

Second, polynomials have awesome properties for constructing MPC protocols, such as additive and multiplicative homomorphisms. That means, adding two polynomials is equivalent to adding the points of the polynomial. When adding shares (which are points), the secrets in the constant terms of the polynomials are also added. A similar property also holds for multiplications: Multiplying two polynomials is equivalent to multiplying points of the polynomial. However, here we have the caveat that the degree of the resulting polynomial doubles from degree-$d$ to degree-$2d$. Hence, $2d+1$ parties are required for reconstructions.

Nonetheless, when introducing a method to reduce the degree of the polynomial after multiplications (see later in this blog post), we can construct a full MPC protocol from this basic technique. Regarding $d$, it is usually chosen to be $\lfloor \frac{n}{2}\rfloor$ to account for the degree growth after a multiplication. Consequently, it is clearly honest-majority since only $\lfloor \frac{n}{2}\rfloor +1$ parties are required to reconstruct secrets.

Replicated secret sharing is a simple, yet powerful, extension to additive secret sharing with the twist that each party has multiple shares. Focusing on the common 3-party case (which is the most efficient one and also the one we use in our implementations), a value $x$ is additively shared as $[x] = (x_1, x_2, x_3)$ such that $x = x_1 + x_2 + x_3$ and each party has two shares: $$ \text{Party}~1: (x_1, x_3) \newline \text{Party}~2: (x_2, x_1) \newline \text{Party}~3: (x_3, x_2) $$ The result is a protocol with the following properties: First, the protocol is clearly honest-majority since the shares of only two out of the three parties are required to reconstruct the secret. Second, since we are operating on additive shares we inherit the property of additive secret sharing that linear functions can be computed on the shares without party interaction. Furthermore, the replication gives a native multiplication protocol: $$ z_1 = x_1 \cdot y_3 + x_3 \cdot y_1 + x_1 \cdot y_1 \newline z_2 = x_2 \cdot y_1 + x_1 \cdot y_2 + x_2 \cdot y_2 \newline z_3 = x_3 \cdot y_2 + x_2 \cdot y_3 + x_3 \cdot y_3 \newline $$ If you do the math, you will see that $z = x \cdot y = z_1 + z_2 + z_3$ works out. Furthermore, Party $i$ can compute $z_i$ locally without interacting with other parties. To summarize, in replicated secret sharing, a multiplication transforms a replicated sharing into an additive sharing and can be computed locally.

Optimizations Based on Multiplications

After the small introduction to the specific protocols, let's now have a look at why they are so efficient. One huge advantage of honest-majority MPC protocols is their simpler multiplication protocols when compared to dishonest-majority ones. They usually follow the same blueprint. First, each party computes a non-interactive multiplication protocol locally. The result usually is valid sharing of the product, but the underlying sharing structure has changed. Then the second part of the protocol is dedicated to restoring the original structure which requires communication. To restore replication, each party sends its share to the next one. To prevent leaking information about the product, the share gets re-randomized before re-sharing, which does not require communication, but more on that later.

In Shamir secret sharing, shares are points on polynomials of degree $d$. A multiplication can simply be performed by multiplying the shares. However, the result is a valid Shamir share of a polynomial of degree $2d$. Thus, a degree-reduction step has to be performed, which also requires fresh randomness (more on that later as well) and communication.

This blueprint of honest-majority multiplications comes with a nice performance optimization for some specific circuits. Note that the intermediate results after the local multiplications are valid secret-shares, although in a different sharing scheme. Thus, when linear operations are performed after multiplications, they can be performed before restoring the original sharing scheme. A concrete example is dot-products $\langle \vec{x}, \vec{y}\rangle = \sum_i^n x_i \cdot y_i$. Instead of computing each multiplication individually which requires communicating $n$ group/field elements for vectors of size $n$, one can perform the local part of the multiplication, do the sum, and re-share/degree-reduce just the result. This approach calculates the correct dot-product but only requires to communicate 1 ring/field element. This strategy is one of the main reasons why the previously mentioned use case with Worldcoin (see the blog) achieves such low communication complexity which directly translates to high performance. Furthermore, this method nicely generalizes to matrix multiplications, and all computations where linear functions are computed after multiplications.

Reducing Communication in Co-Groth16

Looking at a coSNARK prover implementing the well-known Groth16 proving system, this approach allows us to implement the whole MPC-prover with the communication complexity being independent of the number of R1CS constraints. Let's explore how.

In Groth16, the constraint system is represented as a bunch of R1CS constraints (see, e.g. this blog post by 0xPARC for an explainer). This essentially means, the Groth16 prover proves that the following relation is fulfilled: $$ (A \cdot \vec{w}) \odot (B \cdot \vec{w}) = C \cdot \vec{w} $$ Here, $A,B,C\in \mathbb F_p^{n\times m}$ are publicly known matrices describing the constraints, the vector $\vec{w} \in \mathbb F_p^m$ is the private witness vector, and $\odot$ describes an elementwise vector multiplication. In Groth16, one of the first steps is to compress the constraint system into just one vector $\vec{h}$ and commit to it. This compressing is done as follows: \begin{align} \vec{a} &= \mathtt{mulroots}(A \cdot \vec{w}), \notag \newline \vec{b} &= \mathtt{mulroots}(B \cdot \vec{w}), \notag \newline \vec{c} &= \mathtt{mulroots}(C \cdot \vec{w}), \notag \newline \vec{h} &= \vec{a} \odot \vec{b} - \vec{c} \notag \end{align} where $\mathtt{mulroots}(\cdot) = \mathtt{fft}(\mathtt{ifft}(\cdot) \odot \vec{\zeta})$ is a linear function multiplying the input vector with the roots-of-unity $\vec{\zeta}$ in the polynomial domain. As we can see, excluding the matrix-vector multiplications, this step requires $n$ field multiplications, where $n$ is the number of constraints. We exclude the matrix-vector multiplications, since in the MPC setting the matrices are public inputs, thus computing the matrix-vector multiplications does not require communication.

To compress the size of the constraints, in Circom (i.e., the base for our co-Circom implementation) only the matrices $A$ and $B$ are given to the prover. Calculating $\vec{h}$ changes to \begin{align} \vec{a} &= \mathtt{mulroots}(A \cdot \vec{w}), \notag \newline \vec{b} &= \mathtt{mulroots}(B \cdot \vec{w}), \notag \newline \vec{c} &= \mathtt{mulroots}((A \cdot \vec{w}) \odot (B \cdot \vec{w})), \notag \newline \vec{h} &= \vec{a} \odot \vec{b} - \vec{c} \notag \end{align} which results in the equivalent output vector at the cost of a total of $2m$ multiplications instead of $m$ (again excluding matrix-vector multiplications).

In the remainder of the proof creation $\vec{h}$ is just used in a commitment (via a multi-scalar multiplication), which then is added to another shared group element before being published as part of the final proof.

Translating Groth16 to MPC, there are only four parts that require communication:

Calculating the vector $\vec{h}$ as described above.
Multiplying two shared random field elements (denoted as $r$ and $s$ in our implementation).
Multiplying $r$ to a secret group element.
Opening the three group elements that constitute the final proof.

Let's now look closer at the computation of $\vec{h}$ in MPC. Calculating $\vec{a}$ and $\vec{b}$ is linear, and thus requires no communication when evaluated in MPC. However, when $\vec{w}$ is secret-shared, both $\vec{a} \odot \vec{b}$ and $(A \cdot \vec{w}) \odot (B \cdot \vec{w})$ are multiplications of $m$ secret-shared field elements each. When doing a full multiplication (i.e., with degree-reduction in Shamir or re-sharing in replicated sharing), we need to communicate a total of $2m$ field elements for this step. In total, this leads to communicating for $2m+2$ multiplications and $3$ openings to compute the whole Groth16 prover. However, all operations we perform on $\vec{h}$ are linear! The commitment using a multi-scalar multiplication, as well as the share addition is linear, so we do not have to re-establish the original sharing structure after the multiplications in computing $\vec{h}$. We only have to compute the local part of the multiplication (which requires no communication) and can compute the linear functions on additive shares (for replicated sharing) or degree-$2d$ shares (for Shamir sharing). This reduces communication drastically, and we only have to communicate for $3$ openings and $2$ multiplications, a constant number of communicated elements! This is amazing and results in MPC performance being very close to non-MPC performance.

Have a look at the following picture which illustrates this optimization for 3-party replicated secret sharing:

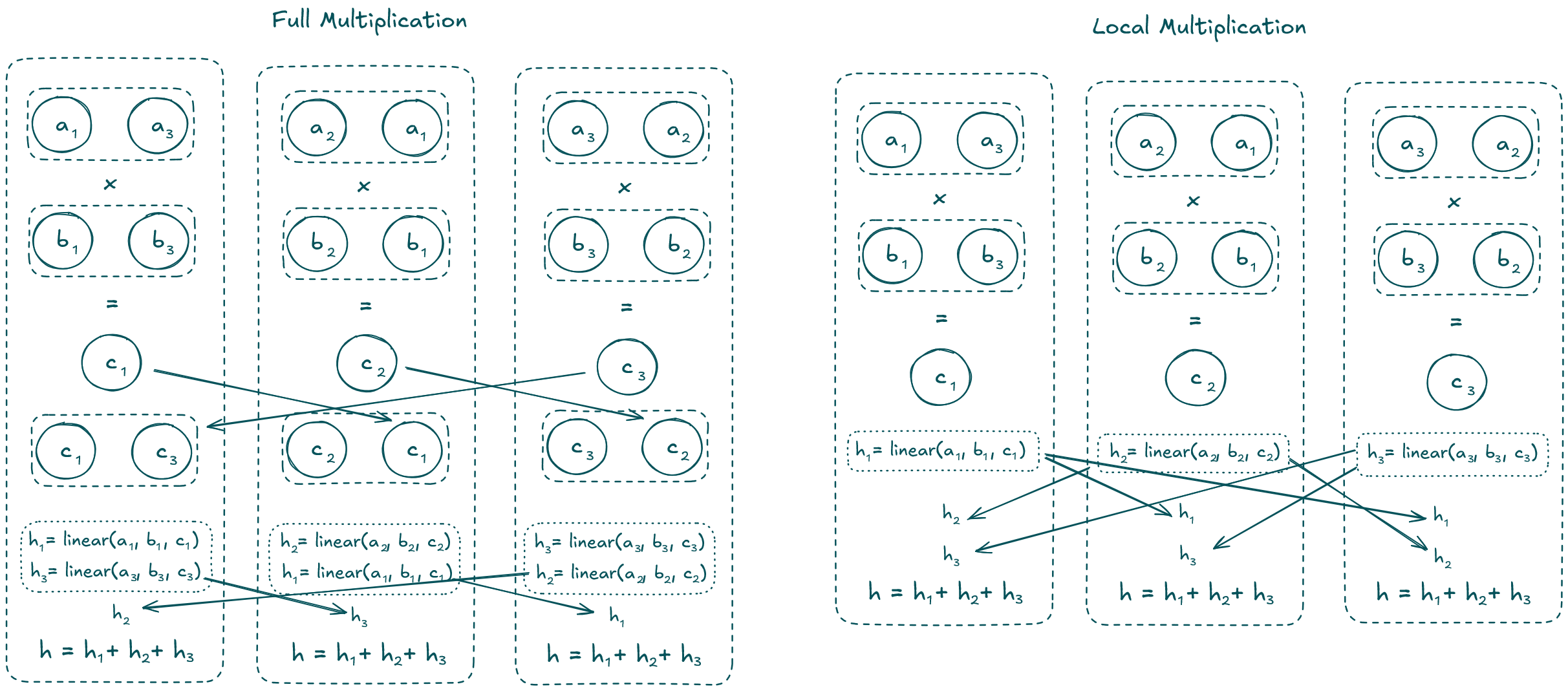
Local Multiplication vs Full Multiplication

Figure 3: Comparison of a full multiplication and a local multiplication for 3-party replicated secret sharing.

Optimizations for Randomness Generation

A common subprotocol in MPC is to jointly generate a random value that remains unknown to all computing parties. This, for example, is required to generate the previously mentioned random values $r$ and $s$ for the co-Groth16 prover. Furthermore, some MPC protocols require sampling unknown random values with special structures. For example, for re-randomizing the result of a local multiplication before re-sharing in replicated secret sharing, parties need to create a fresh additive sharing of 0.

In 3-party replicated sharing, randomness can be created without party interaction. During a setup phase, the parties exchange seeds such that each party has a common seed with both others: $$ \text{Party}~1: (\mathtt{seed}_1, \mathtt{seed}_3) \newline \text{Party}~2: (\mathtt{seed}_2, \mathtt{seed}_1) \newline \text{Party}~3: (\mathtt{seed}_3, \mathtt{seed}_2) $$ These seeds can then be used to create random shares locally since each party can create the correct replication on its own. Furthermore, one can use them to create an additive sharing of 0 (as already observed by, e.g., the influential paper of Araki et. al in 2016), as required by the multiplication protocols. Thereby each party creates their two parts of the random replicated share $[r] = (r_1, r_2, r_3)$, where $r_i$ is generated from $\mathtt{seed}_i$, and subtracts them: $$ z_1 = r_1 - r_3 \newline z_2 = r_2 - r_1 \newline z_3 = r_3 - r_2 \newline $$ It is easy to see that $(z_1, z_2, z_3)$ is a valid additive share of $0 = z_1 + z_2 + z_3$.

Randomness generation is more complicated in Shamir secret sharing. The reason for that is that if each party is generating a random share locally, they do not agree on one degree-$d$ sharing polynomial. In other words, the polynomial created from the shares of the first $d+1$ parties is different (with high probability) from the one generated by the shares of the last $d+1$ parties.

The common approach to overcome this issue is to let each party $i$ locally sample a random value $r_i$ and share it with all other parties. Each party receives $n$ secret shares of $n$ different random values. They can combine these shares into one random value by just simply adding them up. Consequently, they end up with shares of a random value where no party knows the value itself and all parties contributed with fresh randomness. Communication-wise, however, it requires each party to send and receive $n-1$ field elements, which is a lot.

An optimization was introduced in the well-known DN07 paper: Instead of each party summing up the shares it receives from all other parties, they can interpret them as a vector $\vec{r}$ of size $n$ and multiply it to a $(d+1) \times n$ Vandermonde matrix $M$: $\vec{r}' = M \cdot \vec{r}$. As a result, the parties get $d+1$ (where $d$ is the degree of the sharing polynomial), random shares. This works since $d+1$ parties are required to be honest, and their randomness is distributed securely with the Vandermonde matrix. To create $d+1$ random shares with DN07, each party needs to send/receive $n-1$ field elements.

Atlas

Another optimization is described in the Atlas paper. Similar to replicated sharing, seeds can be used to reduce communication: During a setup phase the parties exchange seeds, such that each party shares a seed with the other party, i.e.: \begin{align} \text{Party}~1: &(\mathtt{seed}_{1,2}, \mathtt{seed}_{1,3}, \dots, \mathtt{seed}_{1,n}) \notag \newline \text{Party}~2: &(\mathtt{seed}_{1, 2}, \mathtt{seed}_{2,3}, \dots, \mathtt{seed}_{2,n}) \notag \newline &\qquad \dots \notag \newline \text{Party}~n: &(\mathtt{seed}_{1, n}, \mathtt{seed}_{2, n}, \dots, \mathtt{seed}_{n-1, n}) \notag \end{align}

With these seeds sharing a random value $r$ with the other parties (as is the first step in the shared randomness generation subprotocol) becomes simpler. When party $P_i$ wants to share a random value, $d$ other parties can create them on their own using the seeds they share with $P_i$. $P_i$ can reconstruct a polynomial out of the $d$ shares from the seeds and the random value $r$ it wants to share. Using this polynomial, $P_i$ can then create its own share, as well as the shares of the remaining parties. Thus, this approach requires $P_i$ to send $n-d-1$ shares to these remaining parties instead of sending a share to all $n-1$ parties. With $d=\lfloor \frac{n}{2}\rfloor$, this approach roughly halves the communication.

Remark: Atlas also proposes to extract $n$ random shares from the contributions of each party by multiplying the $d+1$ DN07 shares with another Vandermonde matrix. However, this approach requires changing the so-called king party for each multiplication, making optimized implementation more complicated. Thus, we do not use this optimization in our code.

Degree Reduction for Multiplications

Now to multiplications, i.e., the second part where MPC protocols usually require randomness. So far we have established that a local non-interactive multiplication using Shamir sharing doubles the degree of the sharing polynomial from $d$ to $2d$. In order to chain multiple multiplications, it is required to reduce the degree from $2d$ to $d$ again. The commonly used subprotocol from DN07 is the following. First, parties generate so-called random double shares, a pair of shares where the same random value $r$ is shared as degree-$d$ share and degree-$2d$ share: $([r]_d, [r]_{2d})$. These can be generated by extending the randomness generation protocol with each party sharing the same random value twice, a degree-$d$ share and once as a degree-$2d$ share. Then the parties, in addition to combining the degree-$d$ shares with the Vandermonde matrix, do the same with the degree-$2d$ shares. By each party sending/receiving $2n-2$ field elements, $d+1$ random double shares can be created using DN07.

So how can parties use these double shares for degree reduction of a share $[x]_{2d}$? The approach is simple: $2d$ parties send the value $[x]_{2d} + [r]_{2d}$ to $P_1$ (known as the king party) who can reconstruct the value $x+r$. Since $r$ is fully random and unknown to everyone, $P_1$ does not learn anything about $x$. Then $P_1$ can just simply share $x+r$ as degree-$d$ share and send them to the parties. Finally, each party can subtract its share $[x+r]_d$ by $[r]_d$ and get a degree-$d$ sharing of $[x]_d$.

This approach also allows an optimization: By setting the shares of $d$ parties to $0$, the king-party only has to send out $n-d-1$ shares. This works since $x+r$ is considered fully random, and even though every party can reconstruct $x+r$ using the $d$ zeros and its own share, $x+r$ does not leak anything about $x$. In total, the degree reduction with this optimization requires $P_1$ to receive $2d$ field elements and send out $n-d-1$.

Double Randomness generation with Atlas

To reduce communication, one can apply Atlas' seeds technique also to the generation of random double shares. Generating the degree-$2d$ share works the same as for the degree-$d$ share, thus communication of this share gets reduced from sending/receiving $n-1$ field elements to $n-2d-1$ field elements. Thus, in total, random double sharing only requires each party to send/receive $2n - 3d - 2$ random field elements instead of $2n - 2$ for DN07. Furthermore, observe that if $n = 2d+1$, no communication is required for generating the degree-$2d$ share!

Our Optimization

During the implementation of the Atlas optimization into our coSNARK repository, we came up with another optimization. When party $P_i$ shares a random value $[r]_d$ using the seeds it does not have to choose the random value $r$ itself. Usually, it would use $d$ seeds in combination with its value $r$ to create the sharing polynomial. However, by letting the value $r$ be fully defined by the randomness obtained from $d+1$ seeds, it can reduce the number of parties to interact with by one. The workflow changes to the following. $P_i$ uses $d+1$ seeds (instead of $d$) to generate random shares, thus $d+1$ parties already know their share of $r$ and are not required to receive values. $P_i$ continues by reconstructing the sharing polynomial from these $d+1$ shares, which it can use to calculate $r$, calculate its own share, as well as the shares of the $n-d-2$ remaining parties. Security-wise this optimization does not differ from the case before, since $P_i$ learns $r$ and all other parties just learn their share of $r$.

Have a look at the following illustration:

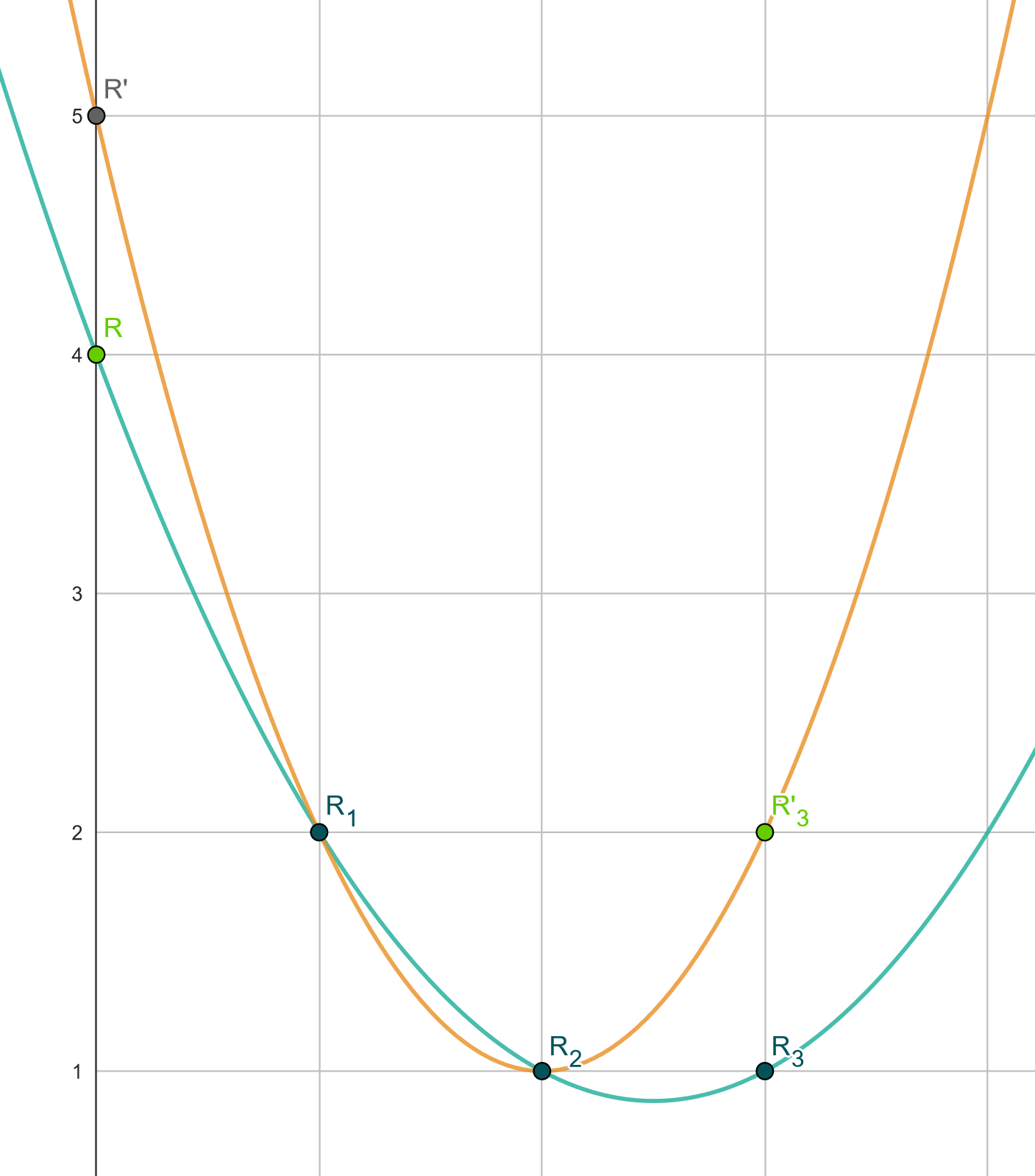
Figure 4: Instead of defining a polynomial (orange line) from a chosen randomness $R'$ and the points from seeds $R_1$ and $R_2$, we let the points $R_1$, $R_2$, and $R_3$ from three seeds define the polynomial (green line) which also sets the randomness to be $R$.

While this optimization reduces the number of field elements sent by $P_i$ by $1$, it cannot be applied to sharing $[r]_{2d}$ in random double shares. The reason for that is, that both shares in random double shares need to represent the same value $r$. If we let $d+1$ shares define $r$ during the creation of the degree-$d$ share, we need to make sure the degree-$2d$ share corresponds to the same $r$. When letting $2d+1$ seeds define the sharing polynomial, its constant term (and thus the share it represents) would with high probability be different from the one chosen for the degree-$d$ share.

Consequently, creating $d+1$ random degree-$d$ share requires each party to send $n-d-2$ field elements, while creating $d+1$ random double share requires each party to send $2n - 3d - 3$. This does, at first glance, not sound too impressive, but when considering the very common case of 3-party Shamir secret sharing (which requires $d=1$), creating random shares and random double shares does not require any party interaction!

This is amazing, and again surprising how similar the properties of 3-party Shamir secret sharing and 3-party replicated sharing are.

Communication for co-Groth16

Summing up, let us now compare the communication for creating a Groth16 proof for a circuit with $2^{20}$ constraints for a trivial MPC implementation without using Atlas seeds and an optimized implementation with local multiplications and Atlas seeds.

	Replicated ($3$)	Shamir ($3$)	Shamir ($n$)
Non-optimized	$6~291~459~\mathbb F$ $12~\mathbb G$	$23~068~691~\mathbb F$ $12~\mathbb G$	$(2^{21} + 1) \cdot (d + n -1) + \lceil \frac{2^{21}+1}{d+1}\rceil\cdot (2n^2-2)~\mathbb F$ $3nd+d+n-1~\mathbb G$
Optimized	$3~\mathbb F$ $15~\mathbb G$	$3~\mathbb F$ $15~\mathbb G$	$n(2n-3d-2)+d-1~\mathbb F$ $4nd+d+n-1~\mathbb G$

Table 1: Total communication for all parties in the different settings for Optimized and Non-Optimized co-Groth16.

Table 1 shows the huge reduction in communication when applying the tricks discussed in this blog post. Not only is communication constant for the whole co-Groth16 prover, but it is also in general super small. Performance is mostly dominated by CPU load, and since all CPU-heavy stuff is linear (FFT, multi-scalar multiplications, etc.), each Shamir party essentially has the same CPU load as a non-MPC Groth16 prover. For replicated sharing, the CPU cost usually is twice that of a non-MPC prover due to computing on two additive shares at the same time. However, using our optimization, some FFTs and multi-scalar multiplications are computed on one additive share instead of replicated shares, reducing the CPU overhead again. As a result, the overhead of going from a Groth16 prover to a co-Groth16 prover is surprisingly small, for both Shamir secret sharing and replicated secret sharing.

Conclusion

Taking a closer look at two specific honest-majority MPC protocols, namely replicated secret sharing and Shamir secret sharing we saw some optimizations that can be made. We showed why these protocols are efficient and how they can be used to significantly reduce communication when used for co-Groth16. As a result, communication is constant, i.e., independent of the number of R1CS constraints, which is both surprising and amazing. Furthermore, we showed where randomness is required in these protocols and how they can be created efficiently. As a result, we once again could see how similar 3-party versions of these two protocols are.

We hope with this arguably mathematically heavier blog post you could gain some insights into optimizations of MPC protocols and how they apply to coSNARKs. Until next time!

Top