Max Pick Challenge – Part 1

TACEO presents the Max Pick Challenge, a unique on-chain guessing game, based on Collaborative SNARKs ("co-SNARKs", leveraging Multi Party Computation + Zero Knowledge) with the chance to win up to $1,000.

The challenge is about submitting a number between 1 and 1000. The one who enters the highest unique guess wins the dollar value in ETH of that guess.

The twist? One of Blockchain’s core features is transparency. Nothing easier than to monitor on-chain activities, reveal which votes were already made and adapt one’s own guess accordingly. However, by leveraging advanced cryptographic techniques like MPC in combination with ZK every guess is made fully private and never shared to anyone (including us!) during the voting period.

999? 800? 501? What do you go for?

Participants are asked to act strategically. They are incentivized to submit a number as high as possible, since the guess directly correlates to the amount paid out. However, if they shoot too high there’s an increased probability that another participant went for the same number, which makes them lose the game. Any number entered more than once is not considered as the unique highest guess. So, for which number will you go for?

Encrypted on-chain guessing

Obviously, any guess submitted in plaintext in the on-chain contract is pointless. The entire game concept wouldn’t work out anymore. We could make use of ZK to store just a commitment of the guess on-chain and, hence, keep it private from others. The user would compute a ZK proof locally making sure the guess is in the required range from 1-1000 and store the guess commitment alongside the proof on-chain, where it can be verified without revealing the guess itself. Instead of public state, which immediately reveals the secret ingredient (the guess), we get private state. That’s similar to how ZK-based privacy chains like Aleo or Aztec work.

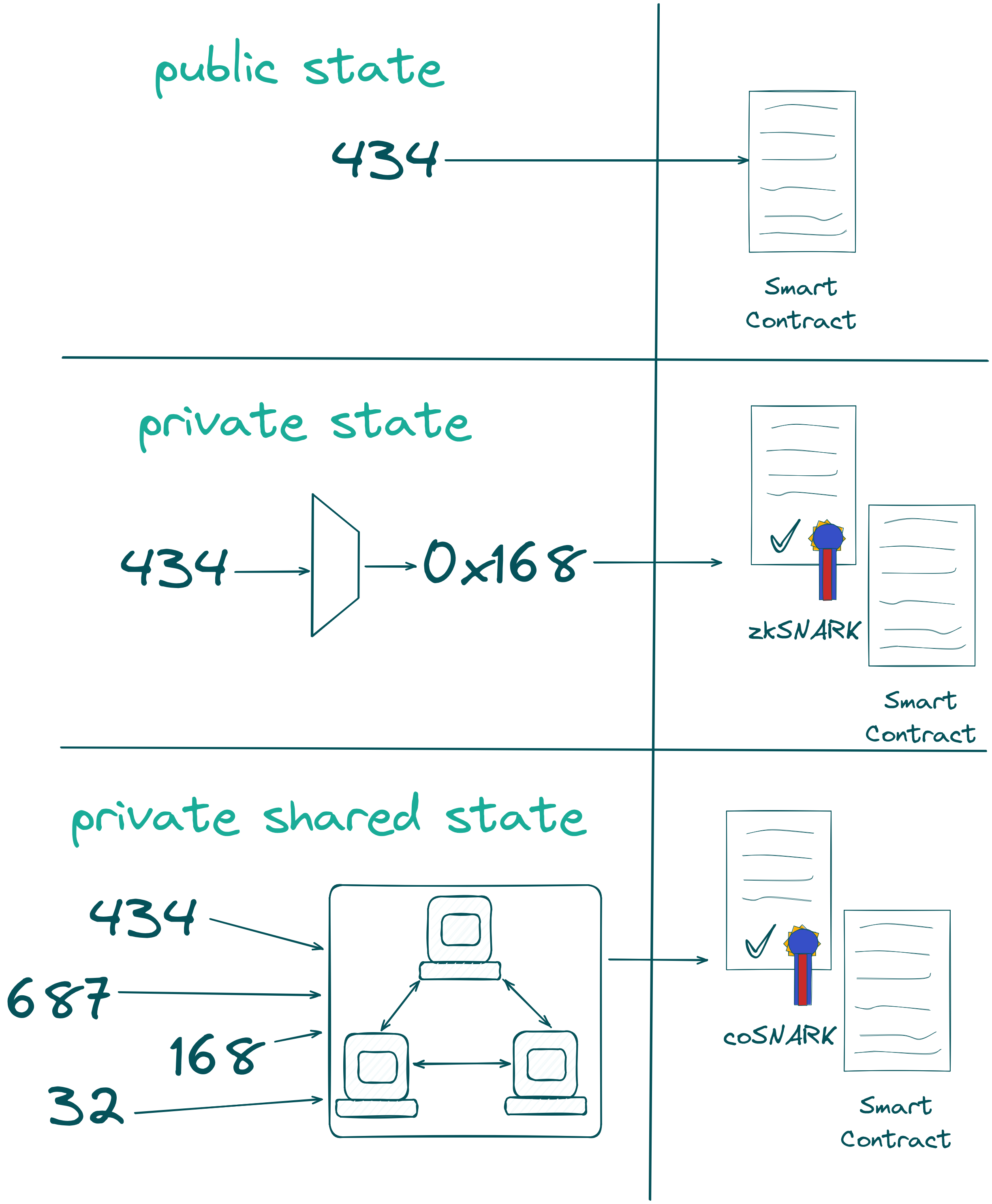
However, the Max Pick Challenge requires us not only to store guesses from multiple users in an encrypted form. It takes us one step further. We need to compute on all of them, without leaking any information about the guesses itself. Multiple private inputs (private state) are taken to perform computations, like in our case, to determine which of the guesses is the single highest one. We’re going from private, independent states to private shared state. Unless we introduce a trusted centralized party, ZK alone isn’t capable of computing on multiple private inputs. We need to combine the privacy-guarantees of ZK with another cryptographic technique: Multi Party Computation (MPC). MPC allows multiple parties to compute an arbitrary function over inputs while keeping those inputs private. In our context, we use MPC to take in private inputs (the encrypted guesses) and compute a function (highest single guess) over them. Throughout this process, ZK gives additional guarantees that the computation by the MPC nodes was done correctly (read more on co-SNARKs).

Architecture & technical overview

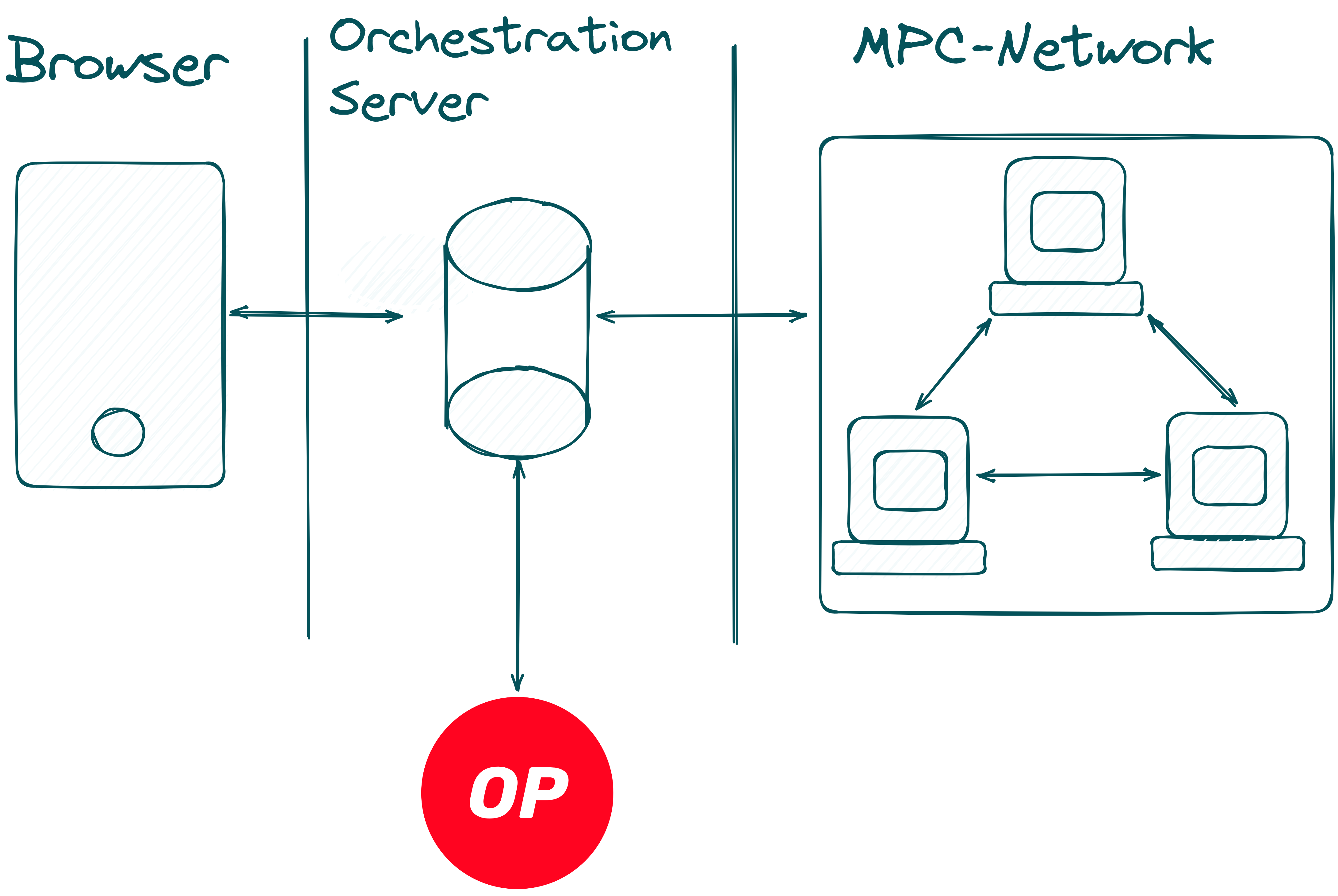
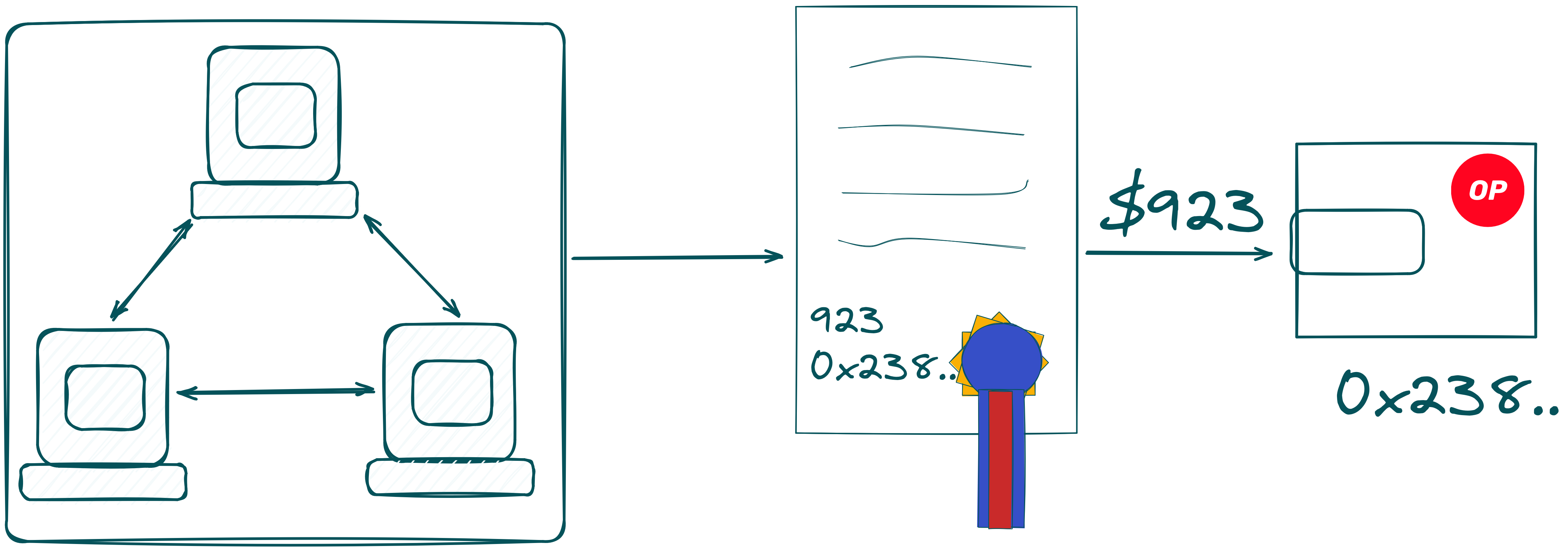
The following description should give a short overview of the tech behind the Max Pick Challenge. A more detailed technical explanation follows in part 2 of this blog post. There are four main components to make the challenge work:

• Orchestration Server: Acts as a relay and persistent storage for the game.
• Browser: The frontend for the game, where users connect with their wallet and submit a guess. It communicates with the Orchestration Server via HTTP requests.
• MPC-Network: A network of MPC (Multi-Party Computation) servers used to compute co-SNARKs¹.
• Smart Contract: A contract on the Optimism mainnet that stores the game's current state and the prize pool.

Step 1 – Making a guess

• The user connects their wallet and submits a guess.
• The guess is secret-shared for the MPC-Network in the user’s browser.
• The browser receives three public keys, each belonging to a party in the MPC-Network. This step is usually handled by a traditional PKI (public key infrastructure).
• The browser encrypts the secret-shared guess using these keys and additionally secret-shares some fresh randomness from the operating system which is required to create a strong commitment later on.
• The browser signs the message with its private key and sends it to the Orchestration Server. Each share is encrypted with its respective key to prevent the Orchestration Server from reconstructing the secret guess and randomness.

Step 2 - Processing the guess

• The Orchestration Server performs sanity checks: verifies the message signature, checks for a positive ETH balance on mainnet (>= $1), and ensures the address hasn’t guessed already.
• The Orchestration Server forwards the encrypted shares to the MPC-Network.

Step 3 – Validating & storing the guess

• The MPC-Network computes a co-SNARK that verifies the guess is between 1 and 1000 and computes a Poseidon commitment to the guess, alongside the address and the additional randomness.
• The co-SNARK is sent back to the Orchestration Server.
• The Orchestration Server forwards the proof to the Smart Contract on Optimism.
• If the proof is valid, the commitment to the guess is stored in the Smart Contract.

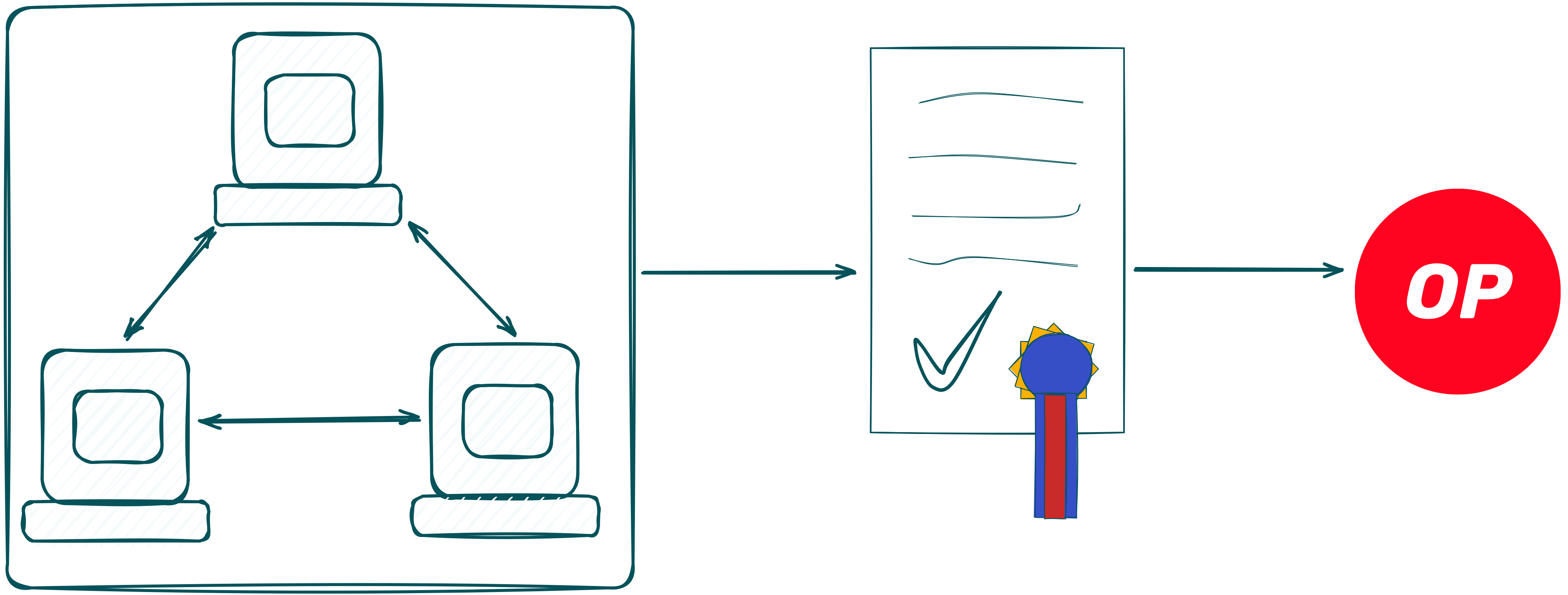
Step 4 - Determining the winner

• The Orchestration Server, which stored all encrypted guesses and randomness in a database, sends the shares to the MPC-Network again.
• The MPC-Network computes another co-SNARK to check all commitments and determine the winner.
• The Orchestration Server receives the result and sends it to the Smart Contract.
• The Smart Contract verifies the proof and awards the prize to the winner. The proof ensures all guesses are accounted for using public inputs provided by the Smart Contract.
• The winner's address and the winning guess are revealed at the end.
• The prize is automatically sent to the winner.

Due to this setup which combines smart contracts and co-SNARKs (i.e., MPC and ZK), each participant can verify that their guess was part of the final computation without ever leaking the guess to the blockchain, us, as the game provider, or anyone else. The challenge is limited to 1,000 participants and will end on Sunday, 14th. Make sure to put out your very own guess and take your chance to win big. Find more details in our FAQ section and follow us on X to get the latest updates.