Hackathon: MHEGA - Make Homomorphic Encryption Great Again

In this 1 week internal TACEO hackathon project, I (Roman Walch, lead cryptographer) wanted to explore the suitability of homomorphic encryption (HE) when applied to our favourite topic: coSNARKs. Obviously, I won't be able to get a full HE-based zero-knowledge proof system running in just one week, but I wanted to create a foundation for some preliminary benchmarks. Thus, I wanted to focus on outsourcing one expensive part of ZK-proof systems: namely FFTs. Let's dive into my results after one week of coding!

Homomorphic Encryption

Let's start with the basics: What is HE? Simply put, HE is a form of encryption which has the additional benefit of allowing to compute functions on encrypted data. The concept of HE is already quite old, the RSA cryptosystem (developed 50 years ago) is, for example, homomorphic for multiplication. In this project I am more interested in modern HE schemes though. These are homomorphic for both addition and multiplication and can thus (in theory) be used to evaluate any function on encrypted data. In practice there are some limitations though:

• HE schemes suffer from huge performance overheads of multiple orders of magnitute compared to the same operations evaluated without encryption.
• Ciphertexts are required to be noisy for security. This means that ciphertexts encode the encrypted messages alongside some noise. This noise grows with every homomorphic operation, slowly for additions and much faster for multiplications. At some point the noise grows large enough, interferes with the encrypted message and decryption will fail. Thus, only a limited number of homomorphic operations are supported. There exists a technique called bootstrapping which resets the noise, but this technique is not applicable for every parameterization of HE schemes (more on that later).

HE schemes

At the moment there exist two different foundational flavours of HE schemes, RLWE-based schemes such as BGV, BFV, and CKKS, and bootstrapping-optimized LWE schemes such as TFHE.

Loosely speaking, BGV/BFV/CKKS have the advantage of allowing large plaintext spaces (most implementation allow up to 60 bit), and allow for packing. The latter essentially means, that one can encrypt a full vector of thousands of elements into just one ciphertext and homomorphic additions/multiplications correspond to elementwise vector addition/multiplication. In other words these schemes natively support SIMD (single-instruction-multiple-data) operations. Furthermore, one can rotate these encoded vectors, even when they are already encrypted. The major downside of these schemes is that bootstrapping is very inefficient. In practice, one often does not use bootstrapping with these schemes and one just uses parameters to support the operations required for a specific use case (this is often referred to as leveled mode).

On the other hand, TFHE's main advantage is its super fast bootstrapping. Indeed, one usually bootstraps after only a handful of operations. However, this comes at the cost of not supporting packing and small plaintext spaces (typically around 8 bits, larger precisions usually require multiple ciphertexts which together encode/encrypt one plaintext).

For a more in-depth introduction to these schemes I shamelessly refer to my PhD Thesis where section 2.2 is fully dedicated to homomorphic encryption.

For my project, I needed to encrypt elements of a large prime field $\mathbb F_p$ with around 256 bits. This already had two implications: I could not use TFHE due to its low precision (and not being able to use CRT-encoding due to working with a prime field), and noise growth will be huge since it scales with the plaintext space.

HE Library

With these limitations in mind, I embarked on the endeavour of finding a suitable HE library for my project. However, the result was sobering: None of the state-of-the-art HE libraries for BGV/BFV¹ (SEAL, HElib, OpenFHE, Lattigo, ...) allow encrypting plaintexts of size >64 bits. So the first goal of my project was set: Extending one of these libraries to allow encrypting my 256-bit prime field elements and thus making HE great (i.e., for big integers) again. After some chats with developers of Lattigo and OpenFHE I decided to shoot my shot with HElib. The reasoning behind this decisions was the following: My chats with the developers discouraged me from using their libraries, I know HElib from my PhD studies and remember it to be very generic, and a paper from 2018 already did something similar with HElib. So I knew it was at least possible, which was very encouraging :).

I thus forked HElib (which implements BGV by the way), rewrote the plaintext modulus to be a biginteger and removed everything unrelated to what I was going to do. The result can be found here. This library alone allows to encrypt large plaintexts (either single prime field elements or polynomials), and supports additions/subtractions/multiplications on ciphertexts.

Rust Interface

Since I love Rust and HElib is a C++ library, the next step of my project was clear: Add a Rust interface to my fork of HElib. For this I first had to add a C-interface² to the functions I needed (see, e.g., c_ctxt.cpp for arithmetic on ciphertexts), which then gets compiled into rust-bindings by my helib-bindings crate. Then, I added the helib-rs crate, which features a nice Rust interface to the created bindings.

Evaluating the FFT on Ciphertexts

After I finally had a usable HE library (in Rust!!!) I was finally able to think about evaluating the FFT. The first instinct might be to just reimplement the FFT algorithms on ciphertexts. However, FFT algorithms have a depth which is logarithmic in their size. Since bootstrapping is not an option for BGV with huge plaintexts, noise growth will be huge, disqualifying this approach immediately.

The second option might be to reinterpret the FFT as a standard matrix-vector multiplication. While this has the advantage of having only a depth of one plaintext-ciphertext multiplication (i.e., manageable noise growth), we have $n$ HE ciphertexts and $n^2$ plaintext-ciphertext multiplications in total for an FFT of size $n$ (which in plain only requires $O(n\log(n))$ multiplications). While having so many ciphertexts requires huge amounts of RAM (especially for large $n$) due to so-called ciphertext expansion, the $n^2$ multiplications will introduce too high performance overheads and scaling. Thus, another option needs to be found...

Luckily there exists an algorithm (we dub it the diagonal method) which allows us to use packing to reduce the number of multiplications and the number of ciphertexts needed. The idea is to extract the diagonals of the FFT matrix, perform an elementwise multiplication with an rotated vector and sum up the results. To use some math, this method can be described as \begin{equation} Z\cdot \vec{x} = \sum_{i=0}^{n-1} \texttt{diag}(Z, i) \odot \texttt{rot}(\vec{x}, i) \end{equation} where $\texttt{diag}(Z, i)$ extracts the $i$-th diagonal of the matrix $Z$, $\texttt{rot}(\vec{x}, i)$ rotates the vector $\vec{x}$ by $i$ steps, and $\odot$ describes an elementwise vector multiplication. See the following depictions of the $n=4$ case:

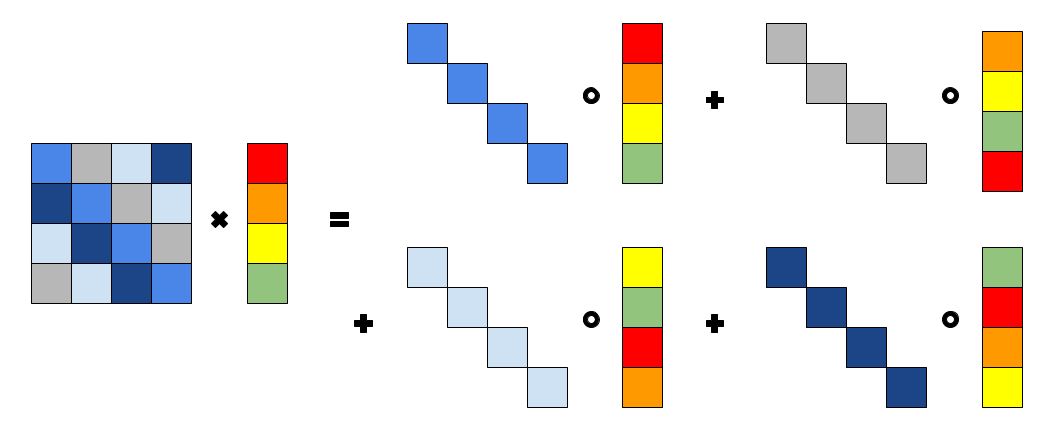
Furthermore, the number of rotations can be reduced by using the babystep-giantstep optimization (see, e.g., page 19 of this paper).

The result is that only $n$ plaintext-ciphertext multiplications, $n-1$ additions, and $O(\sqrt n)$ rotations are required to evaluate the plaintext-matrix times encrypted-vector multiplication. Using this method, however, requires me to get packing and rotations running with my HElib modification. Oh boy...

Packing and Rotations

Let us start with some theory. Feel free to skip this section and join back later on if you are not into this kind of math :)

So, plaintexts in BGV are in general polynomials $\in \mathbb Z_p[X]/\Phi_m(X)$ where $\Phi_m(X)$ is the $m$-th cyclotomic polynomial with degree $\varphi(m)$. Thus, our plaintexts are polynomials of degree $\varphi(m)-1$ where the coefficients are integers mod $p$. In case we just want to encrypt one field element, we can just put it in the constant term of the polynomial and proceed. However, with packing we have the opportunity of encoding a whole vector of size $\varphi(m)$ into a polynomial, where polynomial addition/multiplication (and thus also homomorphic addition/multiplication once encrypted) correspond to elementwise vector operations³. Each encoded value will then correspond to one root of the reduction polynomial $\Phi_m(X)$. Furthermore, since $\Phi_m(X)$ has powers of the $m$-th root of unity as its roots (concretely, let $\xi$ be the $m$-th root of unity, the roots of $\Phi_m(X)$ are all $\xi^i$ where $i\in \Z_m^*$, i.e., gcd$(i, m) = 1$), we can use Galois automorphisms $\tau_i: \xi\mapsto \xi^i$ to permute the roots which corresponds to permuting the encoded vector.

In general one can build some types of vector rotations from these automorphisms. Unfortunately though, we cannot get a cyclic rotations over the full vector and the concrete rotation structure is in general a so-called "hypercube" which depends on $m$. Luckily, the most efficient case where $m$ is a power-of-two⁴ has a decent rotation structure. First, this case leads to $\Phi_m(X) = X^{m/2} + 1$, thus one can use a negacyclic NTT for encoding/decoding. Second, since $\Z_m^* \simeq \Z_{m/4} \times \Z_2$, i.e., we can rewrite $i\in \Z_m^*$ to $i=g_1^{j_1} g_2^{j_2}$ with $j_1 \in \Z_{m/4}$ and $j_2 \in \Z_2$. Consequently, our Galois automorphisms allow to move encoded values alongside two generators $g_1$ and $g_2$, where $g_1=3$ and $g_2= m-1$ are known to be usable for this case. Long story short, we can encode a vector of $m/2$ elements into a matrix of 2 rows with $m/4$ elements each and can use Galois automorphisms to either rotate both rows simultaneously (move elements alongside $g_1=3$) or swap the rows (move elements alongside $g_2=m-1$). To visualize: When encoding two vectors $\vec{a}_1$, $\vec{a}_2$ of size $m/4$ each, Galois automorphisms do the following:

\begin{align} \text{Encode}\left(\begin{bmatrix} \vec{a}_1 \\ \vec{a}_2 \end{bmatrix}\right) = a \in \Z_p[X]/\Phi_m(X): \quad &\text{Decode}(\tau_{3^i}(a)) = \begin{bmatrix} \texttt{rot}_i(\vec{a}_1) \\ \texttt{rot}_i(\vec{a}_2) \end{bmatrix}, \notag \\ &\text{Decode}(\tau_{m-1}(a)) = \begin{bmatrix} \vec{a}_2 \\ \vec{a}_1 \end{bmatrix}. \end{align}

Furthermore, Galois automorphism are homomorphisms per definition which is why they can be applied to HE ciphertexts as well. Concretely, a ciphertext in BGV is usually represented as two polynomials $(c_0, c_1)$ where $c_0, c_1 \in \Z_q[X]/\Phi_m(X)$ for some ciphertext modulus $q\gg p$. Decryption is defined as $c_0 + s \cdot c_1 = m + p\cdot e$, where $s$ is a secret decryption key polynomial, $m$ is the plaintext polynomial, and $e$ is the noise polynomial (which gets removed by reducing mod $p$). Applying Galois automorphisms leads to the following (while abusing notations a little bit): \begin{align} \tau_i(c_0 + s \cdot c_1) &= \tau_i(m + p\cdot e) \notag \\ \Leftrightarrow \tau_i(c_0) + \tau_i(s) \cdot \tau_i(c_1) &= \tau_i(m) + p\cdot \tau_i(e) \end{align} Hence, applying $\tau_i$ to both ciphertext polynomials leads to the application of $\tau_i$ to the plaintext polynomial while noise is still removable by a reduction mod $p$. However, the resulting ciphertext is now decryptable by $\tau_i(s)$ instead of $s$. Consequently, the ciphertext needs to be transformed by a so-called keyswitch operation which makes it decryptable by $s$ again. This operation requires a keyswitching key KS$_{{\tau_i(s)}\rightarrow s}$ which needs to be created by the party knowing $s$ for each index $i$.

Implementing Packing and Rotations

Welcome back everyone skipping the previous section! Long story short: In order to implement packing and rotation for the parameters $\Phi_m = X^{m/2} + 1$, with $m$ being a power-of-two (the most common and efficient case), I needed to implement encoding via a negacyclic NTT, creating keyswitching keys and implement Galois automorphisms. Luckily, HElib already implements the required functionalities for creating keyswitching keys and applying automorphisms, so I only added a wrapper class for my convenience. For the encoding, I implemented the NTT in Rust.

One more thing I need to mention which is a result of the weird rotation structure of the previous section: For FTTs with size $m/2$ I need to split the matrix into 4 submatrices to efficiently make use of the packing: \begin{equation} M = \begin{bmatrix} M_1 & M_2 \\ M_3 & M_4 \end{bmatrix} \quad \vec{x} = \begin{bmatrix} \vec{x}_1 \\ \vec{x}_2 \end{bmatrix} \end{equation} leads to \begin{equation} M \cdot \vec{x} = \begin{bmatrix} M_1 \cdot \vec{x}_1 + M_2 \cdot \vec{x}_2 \\ M_3 \cdot \vec{x}_1 + M_4 \cdot \vec{x}_2 \end{bmatrix} \end{equation} which can be implemented by calling the diagonal method twice. See my implementation (in Rust) for different matrix sizes here.

Results

Finally, after all this math and implementations let's have a look at some results. First, let us inspect my BGV parameter choices to evaluate FFTs in the BN254 scalar field⁵ homomorphically. As hinted in the beginning of this blog post, noise growth is quite large due to the huge plaintext prime modulus (~254 bit) we need in this project. Despite only evaluating a circuit with a depth of one plaintext-ciphertext multiplication, noise grows by 540 bit! As a consequence, I had to instantiate the ciphertext modulus $q$ with 1045 bit to accommodate for this large noise growth. Finally, the choice of the cyclotomic polynomial $\Phi_m(X)$ impacts the security of the HE scheme: The bigger the degree, the better. Since I am forced to use a power-of-two $m$, and choosing $m=65536$ leads to only ~71 bit security (according to the lattice estimator), I needed $m=131072$ giving me ~194 bit of security. Thus, my reduction polynomial was $X^{65536} + 1$ allowing me to pack 65536 field elements into one ciphertext.

Benchmarks

Now I will present some benchmarks for evaluating FFTs (see the Rust source code here) with different sizes on a packed HE ciphertext and compare it to the FFT without encryption (Plain). The benchmarks are single-threaded and were taken on a server with an AMD Ryzen 9 7950X CPU (base clock 4.5 GHz) and 100 GB of RAM.

FFT Size	HE FFT (s)	Plain FFT (s)
256	20.3	0.00003
512	38.6	0.00007
1024	71.3	0.00015
2048	138.2	0.00032
4096	262.2	0.00069
8192	506.7	0.00151
16384	954.3	0.00464
32768	1514.2	0.01235

The results are somewhat sobering. The overhead of homomorphic encryption is more than 6 orders of magnitude despite using the optimized algorithms for evaluating the matrix-vector multiplications. A still comparably small FFT of size 32768 blows up from 12.35 ms without encryption to 1514.2 s with encryption. This is rough, especially when comparing it to MPC which does not add any overhead to FFT computations due to its linearity (see our blog post).

Unfortunately, CPU overhead is not the only drawback of using HE, RAM requirements are also huge. The final benchmark with size 32768 required nearly everything of the 100 GB RAM of the benchmark server. The reason for that is (among the general size of HE ciphertexts) the size of the many key-switching keys required to evaluate all the ciphertext rotations in the babystep-giantstep optimized diagonal method. These need to be created by the party knowing the decryption key, thus, when HE is used for outsourcing computations, the communication of these keys already requires to upload several tens of GBs of data.

Conclusion

Overall I have to say I enjoyed working with homomorphic encryption again, it reminded me of some exciting times during my PhD. Unfortunately though, HE is still quite slow and my results of just evaluating FFTs with HE show that HE is not really a feasible alternative to MPC for coSNARKs. Let's just hope that future research and hardware acceleration will bring performance overheads of HE down a bit to make it usable for a broader range of use cases. Until then (and probably still afterwards) we can be happy to have a fast and feasible alternative with MPC where FFTs, depending on the concrete protocol, only add negligible overhead to the plain computation. Happy holidays!

---

---

Thank you for following our hackathon series! If you'd like to read more about coSNARKs and the rest of the TACEO stack, feel free to check out the docs, chat with us in Discord, and follow for news on X!