MPC GeoTools: Private Computation with GPS Coordinates

Hey! I'm Fabian Gruber and for our TACEO hackathon I chose to implement a tool for private computation with location data based on Multi-Party Computation (MPC).

Computation based on your or others' GPS coordinates (latitude and longitude) happens all the time, and many things, such as location-based weather reports, dating apps, etc., depend on it. However, in terms of privacy, this is a nightmare. Your location gets shared with countless companies from all over the world, often without your knowledge. This goes so far that even some calculator apps request access to your location.

That's where Multi-Party Computation comes into play. By leveraging MPC, we can still perform sensitive computations, such as the distance to some other party/location, without revealing the actual data (our location) to any 3rd party. This approach ensures that privacy is maintained throughout the process while still enabling accurate and useful results.

I implemented MPC GeoTools, a prototype for private two-party computation with GPS coordinates. Both parties use additive secret sharing¹ to split their coordinates into shares. All computation is performed on those shares. The project uses GeoJSON as input and output format. This makes it easy to use existing tools such as geojson.io to visualize the results.

Private Distance Computation between two Parties

You want to compute the distance between you and another party. But neither of you wants to reveal their location. Instead, you can compute the great-circle distance with secret-shared GPS coordinates.

$$ \begin{align*} \Delta x &= \cos \phi_2 \cos \lambda_2 - \cos \phi_1 \cos \lambda_1 \\ \Delta y &= \cos \phi_2 \sin \lambda_2 - \cos \phi_1 \sin \lambda_1 \\ \Delta z &= \sin \phi_2 - \sin \phi_1 \\ \Delta c &= \sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2} \end{align*} $$

Using the formula for the chord length and approximations for $\sin$, $\cos$², and by getting rid of the sqrt of a secret value (since the distance gets revealed anyways, we can just reveal $c^2$ and do sqrt in plain), we get a pretty accurate result for the distance $d = c \cdot R$ (where the mean earth radius $R \approx 6371 km$).

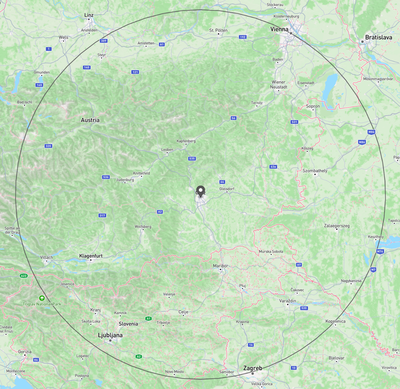
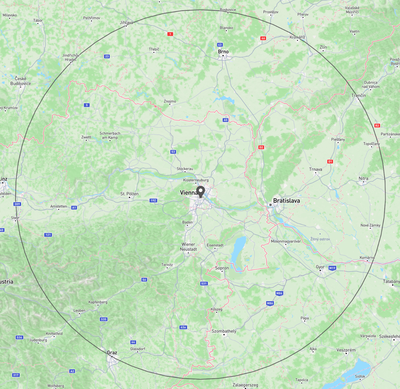
In this example, one party is in Graz, and the other party is in Vienna. The computed distance is $144.55 km$ and the actual distance is $144.51 km$. That's pretty close! In the pictures below, you can see the viewpoints of both parties. They only learn that the other party is a certain distance $d$ away, but not where exactly they are on the circle with $r = d$.

Private Distance Threshold between two Parties

We can extend the secret distance computation from above to a threshold check by comparing $c^2$ to a $t = (\frac{\text{threshold in km}}{R})^2$ (scale the distance threshold so we can compare to $c^2$). This allows a party to find out if the other party is within a distance threshold (public or secret) but nothing more about their location.

Private Point in Polygon

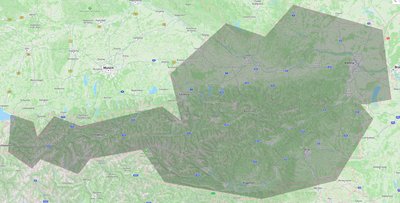
Another interesting problem we can solve is checking if a party is in a specific area given by a polygon. This can be used for, e.g., finding out if a party is in a specific continent/country/city or not. To achieve this, we transform the latitude and longitude coordinates into x and y coordinates using the Mercator projection. Then we can perform a point inside polygon check with secret-shared coordinates (expensive because we have to make a lot of comparisons³, scales with the number of vertices in polygon). In the end, you only learn if the other party is inside the given polygon.

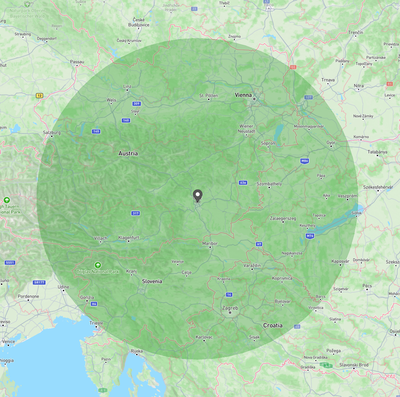
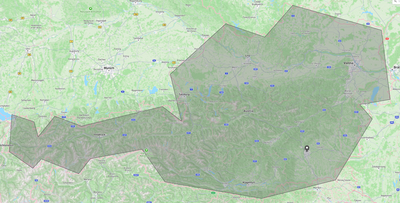
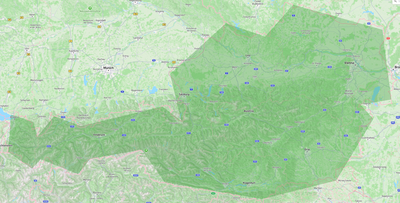
With the following polygon and location, the check returns true because party 0 is inside Austria:

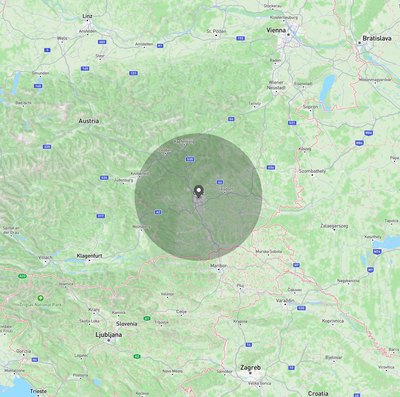
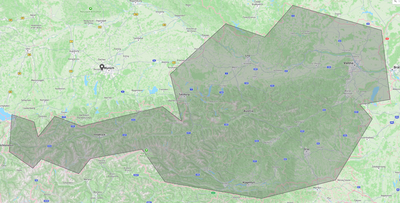
With the following polygon and location, the check returns false because party 0 is outside Austria:

Conclusion

I had a lot of fun implementing this prototype during the TACEO hackathon, and I am happy with the result. Hopefully, this project can highlight the potential of MPC in a variety of applications, particularly in scenarios where privacy concerns are paramount. Who knows, maybe it will lead to something more than just a prototype.

---

---

Thank you for following our hackathon series! If you'd like to read more about coSNARKs and the rest of the TACEO stack, feel free to check out the docs, chat with us in Discord, and follow for news on X!