on
Multiparty Notaries for zkTLS
It's not often you can say that a topic in this area has been worked on for more than 10 years, but zkTLS is one of them. It arose to solve a problem at the intersection of privacy, trust, and verifiability—allowing users to prove facts about TLS-secured data without revealing the underlying content.
Initially proposed in Bitcoin forums in 2013, the idea fueled projects like TLSNotary and gained practicality through approaches in projects such as Opacity, vlayer, Reclaim, Pluto, and Clique. Today, zkTLS has evolved into a key cryptographic tool for building usable DeFi, identity solutions, and beyond.
What is zkTLS?
Simply speaking, zkTLS generates a cryptographic proof on the contents and integrity of a TLS session—without revealing the actual data. This proof allows a verifier to confirm that a specific statement about the session—such as an account balance, transaction confirmation, or the presence of specific data—is true while keeping the underlying details private.
Why this matters now
As zkTLS increasingly finds product-market fit, securing higher-value applications, it's crucial to adopt solutions that can withstand larger threat surfaces. Real applications are emerging, securing increasing amounts of value, and being integrated into high-stakes use cases. With this growth, the security assumptions underpinning these protocols matter more than ever. While there are multiple ways to generate zkTLS proofs, some approaches introduce trade-offs that become more concerning as the stakes rise.
Why choose MPC
You might wonder—why not just compute a ZK proof ourselves? Why involve a second party at all? Unlike other ZK applications like email proofs, the client in a TLS session knows the encryption key the server will use for responses and could forge arbitrary ciphertexts. To add verifiability to TLS, some form of trusted infrastructure is needed to produce or notarize the proofs.
There are several types of infrastructure to generate these proofs. Some approaches rely on proxy-based solutions, where a trusted intermediary establishes the TLS session and attests to its contents. Others use trusted execution environments (TEEs) like Intel SGX to generate proofs inside secure hardware. While these methods can be practical, they introduce centralization risks, hardware dependencies, and reliance on a single entity. Each method has different trade-offs in terms of security, trust assumptions, and performance. For a deeper dive on the different approaches, you can see the vlayer Web Proofs report.
The MPC-based approach, on the other hand, offers a decentralized alternative. Instead of a single entity handling proof generation, multiple parties jointly compute the proof without any one party having full visibility into the session data. This eliminates the need for trusted intermediaries, reducing censorship risks and reliance on specific hardware. It also aligns well with cryptographic security principles, avoiding vulnerabilities like side-channel attacks. More importantly, it's the approach we know best and have the most experience with.
However, traditional MPC-based TLS protocols rely on two-party computation (2PC) between a client and a single notary which introduces some limitations.
First, trust assumptions are weaker. With only one notary, there’s nothing preventing it from colluding with the client to generate false proofs. The security model assumes the notary is always honest, creating a single point of failure.
Second, censorship and availability risks emerge. A single notary could refuse to cooperate, censoring users by preventing proof generation. If that notary is compromised or taken offline, the system stops, introducing dependencies on centralized infrastructure.
The path forward: moving beyond 2PC
There are also non-cryptographic approaches to solving these issues, as seen in Opacity’s work, outlined in a great talk that is unfortunately not available anymore on YouTube (https://www.youtube.com/watch?v=c8_ii_rgl1a). However, a cryptographic approach offers greater versatility by eliminating the need for static IDs. With this in mind, the natural question arises: Can we extend the client to more parties?
If so, it would eliminate the risks of collusion and censorship while introducing new benefits, such as the economic incentives used by Opacity, and stronger security guarantees. Here, we explore how to further decentralize notaries for zkTLS while maintaining strong security guarantees. We sketch a solution for a multiparty garbled circuit approach—but first, let’s go back to the beginning.
Primer on MPC-TLS
Our main goal is to MPC-ify the client of a TLS connection:
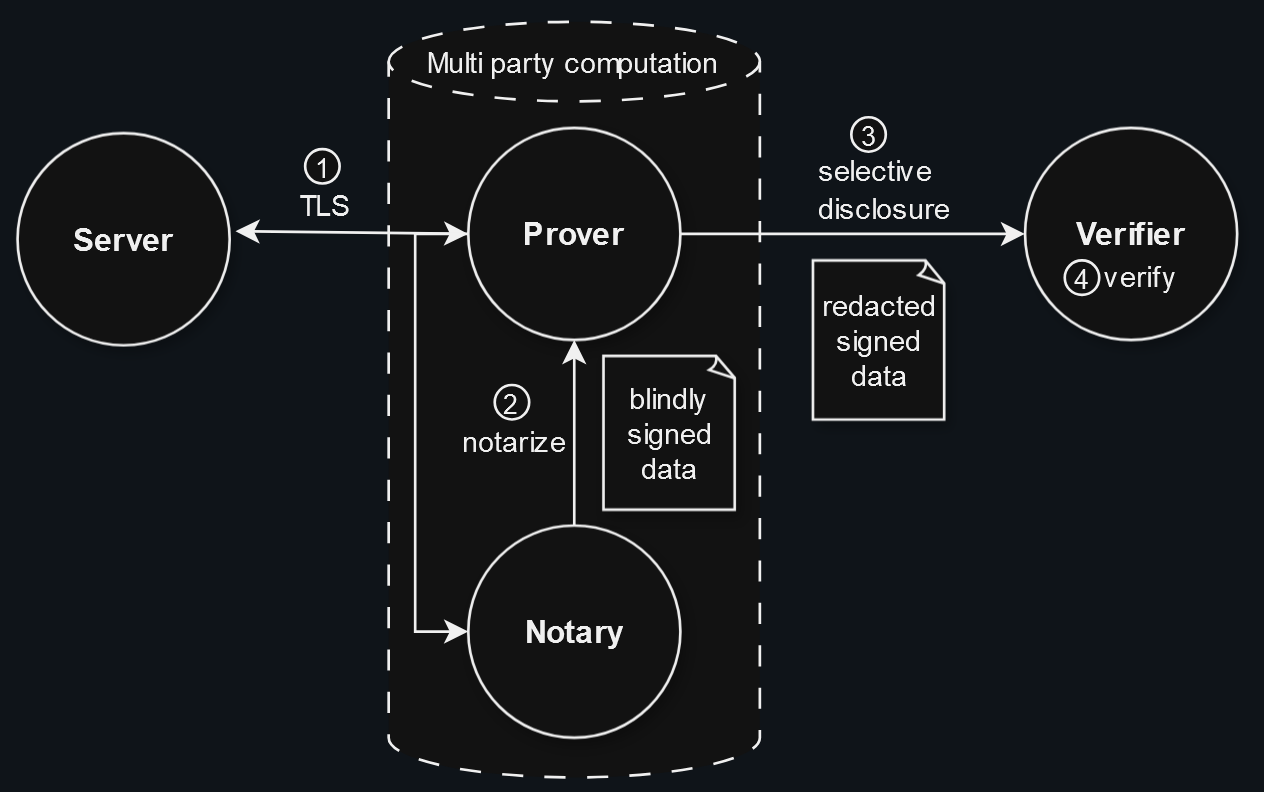
Image 1: TLS Notary Architecture (from tlsnotary.org)
This introduces two key challenges:
- Server Transparency – The TLS server should be oblivious to whether the connection is using MPC-TLS or standard TLS, as it is impractical to require all web servers to support notarization.
- Client Integrity – The client should be prevented from manipulating the process to generate fraudulent proofs.
To ensure security, the TLS connection must be set up in a way that prevents the client from knowing the TLS session keys. The standard approach is to use MPC to split control of the session between the client and a notary. Together, they perform the TLS handshake and encrypt/decrypt data through an MPC computation. Since neither party holds the full encryption keys—only secret shares of them—they must collaborate to process any data. Additionally, the notary signs cryptographic commitments to specific content (e.g., a bank balance), which can later be used in attestations or zero-knowledge proofs.
As is always the case with MPC, the protocol is just secure if the MPC-parties do not collude. Consequently, a multiparty setup with multiple notaries is preferable over a setup with just one notary.
MPC-TLS issues
The biggest issue with an MPC-ified TLS client is the very strict performance requirement of the server expecting the TLS-handshake to be finished in a specific time frame (usually between 8 and 30 seconds, depending on the concrete implementation)-otherwise it will abort the connection. Computing the handshake requires the server and the client to
- agree on a pre-master-secret key using Diffie-Hellman,
- derive session keys (requires ~20 SHA-256 evaluations using TLS1.2 with the TLS_ECDHE_ECDSA_WITH_AES_128_GCM_SHA256 cipher suite, TLS1.3 will require more hash evaluations),
- finish the handshake with an encrypted message (requires some AES-GCM evaluations).
MPC-ifying the client requires evaluating all these primitives in MPC. Especially the symmetric ciphers (AES) and hash functions (SHA256) used in TLS are known to be pretty MPC-unfriendly [1]. Using secret-sharing based MPC protocols (SPDZ, Rep3, Shamir, ect.) would require several thousand communication rounds to compute the whole handshake which makes it nearly impossible to achieve the strict latency requirements imposed by the server-especially with high-latency internet connections between the MPC nodes. Thus, existing solutions (e.g., TLSNotary) primarily focus on garbled circuit implementations, which have the advantage of having a very low number of communication rounds.
The key disadvantage is that garbled circuits usually are used as two-party protocols limiting the number of notaries to just one.
Extending to multiple notaries
The common wisdom about multiparty garbled circuits is that they introduce huge communication overhead compared to 2-party garbled circuits (which already have higher communication compared to secret-sharing based MPC protocols), and malicious security (i.e., detecting whether MPC parties cheat during evaluation) adds another layer of huge overhead. Consequently, we thought it would be very unlikely to achieve the strict timeout requirements with a multiparty garbled circuit setting.
Yet, behold the paper Global-Scale Secure Multiparty Computation: Its multiparty garbled circuit protocol has some properties which makes us believe a MPC-TLS with multiple notaries is feasible!
First, the protocol introduced in this paper splits execution into input independent offline phases and a very cheap input-dependent online phase. In MPC-TLS, the more expensive offline phase can be computed before the TLS connection is initiated. Consequently, only the online phase must be finished during the strict timeout period for the server.
Second, the protocol achieves malicious security without cut-and-choose, reducing the overhead significantly.
Finally, the protocol achieves security with dishonest majority, i.e., only one notary needs to be honest to detect malicious behavior. This is a huge gain compared to the usually more efficient (and thus more common) setting of honest majority, where a majority of notaries would be required to behave honestly.
Let's look at some benchmarks from this paper. They distinguish execution for multiple parties in a LAN setting (fast and low-latency network connection) and a WAN setting (slow and high-latency network connection). The full benchmarks are present in Appendix C of the paper. As an example, for 8 parties (i.e., 7 notaries) evaluating one SHA-256 hash requires in total 2s in the LAN setting, while requiring 12.6s in the WAN setting. Crucially though, online runtime is just 115ms in the LAN and 185ms in the WAN setting.
This is incredible, especially when considering that when the paper was written, an unfavorable garbled circuit for SHA-256 was used which requires too much communication. A better circuit was introduced in this paper, which reduces the number of AND gates (the parts requiring communication in garbled circuits) by a factor of 4. The public implementation of the paper found here already was updated to include this new circuit.
Scaling up for 20 SHA-256 evaluations as required by the TLS1.2 handshake, online time will just be 2.3s in the LAN setting and 3.7s in the WAN setting. This should be fast enough to execute the remaining TLS operations in time as well (which we describe in the next sections of this note). The total time of the garbled circuits, according to the paper, for the 20 SHA-256 hashes will be 40s in the LAN setting and 252s in the WAN setting (with the old SHA-256 circuit requiring too much AND gates).
For completeness, the total communication for this example of 20 hashes with the older circuit in the paper would be 4.6 GB, from which 180kB have to be communicated in the online phase.
Putting the protocol together
Having this cool paper in mind, let's put together all MPC protocols required for the TLS handshake.
Key exchange
The key exchange is used to establish a common secret between the TLS server and client using Diffie-Hellman which is then used to derive session keys. In essence, we propose a similar protocol as described in TLSNotary.
First, each notary and the client have/pick their own key pair $(sk_i, pk_i = sk_i \cdot G)$. They send the sum of their public keys $pk = \sum_i pk_i$ to the server and receive the public key of the server $pk_s$. Each client/notary now computes $Q_i = sk_i \cdot pk_s$. The desired pre-master-secret would then be the x-coordinate of the point $Q = \sum_i Q_i$. This sum is over elliptic curve points, hence point addition boils down to $(x_a, y_a) + (x_b, y_b) = (x_r, y_r)$ with $x_r = \lambda^2 - x_p -x_q$, $y_r = \lambda \cdot (x_a- x_r)- y_a$, while $\lambda = \frac{y_b-y_a}{x_b-x_a}$. This requires in total three multiplications and one inversion per point addition (for which we need $n-1$ for $n$ parties).
We propose to simply use SPDZ as the MPC protocol for this step.
Furthermore, since we do not reconstruct the final result (it will be an input to the garbled circuits in the next step), we expect (at least the online phase) of this step only requires semi-honest security. The reason is that a faulty computation will be detected later by the TLS server since wrong keys are derived, and sensitive data cannot be leaked since no (non-encrypted) data is ever reconstructed. For a final implementation, though, this conjecture needs to be further investigated. Nonetheless, even if malicious security is required here we should not run into server-timeout problems since the expensive part has to happen in an input-independent offline phase (the online phase is only twice as expensive for SPDZ plus MAC-check).
Bridging to Garbled Circuits
The next step in TLS is deriving session keys from the established pre-master-secret. As discussed before, we would like to use the multiparty garbled circuit protocol from the paper Global-Scale Secure Multiparty Computation for this step. Consequently, we need to input the secret shares from the previous step into the garbled circuits. Our proposed approach is that each party (client and notaries) just uses their secret share of the pre-master-secret as input to the garbled circuits. Consequently, before any SHA-256 hashes can be computed inside the garbled circuits, the pre-master-secret needs to be reconstructed from the input secret shares. This boils down to $n-1$ additions in the field $\mathbb F_p$, where one of these additions requires two ripple-carry adders and cmuxing the outputs with a total of roughly $3\cdot \lceil\log_2(p)\rceil$ AND gates per finite field addition.
The proposed approach also only provides semi-honest security, since the parties could input shares that differ from the ones derived in the previous step. This is equivalent to adding an offset to the key. However, doing this results in wrong session keys being derived in the later parts of the protocol which gets detected before any data is opened (keep in mind the actual garbled circuit computation is malicious secure, so only an encryption with an unknown but modified key will be reconstructed to the MPC parties, which will get rejected by the server). Thus, we currently believe, that only having semi-honest security here is no issue.
Session Key derivation
After the shares are reconstructed inside the garbled circuits, the session keys can be derived by evaluating ~20 SHA-256 hashes inside the garbled circuit. The keys will not be reconstructed, but kept as wire labels for further computation. As mentioned before, the garbled circuit evaluation itself provides malicious security with a dishonest majority.
Data Encryption/Decryption
Finally, for encrypting messages and decrypting responses we would also propose using the garbled circuits. Indeed, the benchmarks of AES indicate them to be faster compared to SHA-256, while GHASH (used for GCM) should also be efficient enough (8765 AND gates per finite field multiplications according to https://eprint.iacr.org/2023/964.pdf).
Conclusion
We've discussed how TLS-MPC with multiple parties can be realized while keeping the (online) performance fast enough to not run into timeout issues. An implementation of this approach would require implementing the multiparty garbling protocol from Global-Scale Secure Multiparty Computation, or using its implementation found here. Furthermore, we propose to keep some steps, concretely the key exchange step, semi-honest, which should be more carefully considered before deployment in practice.
We would like to express our thanks to the several zkTLS teams and academics who validated our ideas. If you are a team interested to work this topic, don't be shy to get in touch.
[1] There is a whole research area introducing symmetric primitives optimized for MPC, ZK, FHE. Examples include LowMC, MiMC and Poseidon.
Thank you for reading our blog! If you'd like to read more about our MPC protocols, coSNARKs, or other TACEO tooling, feel free to sign up to our newsletter, chat with us in Discord, and follow for vibes on X!