on
Poseidon{2} for Noir
It has been some time since our last blog post (3 months already, time flies) - so it is way overdue to continue our loose series of blog posts about zk-friendly hashing. In case you missed the other two posts, feel free to read about how to choose your zk-friendly hash function and ask yourself, 'What's the deal with hash functions in Zero Knowledge'. While this is an ongoing series of related blog posts, it is not necessary to read others in this series before this one. It will only take $\approx 10$ minutes though and will give you a good overview on the topic.
While the other blog posts were more theoretical, this one will be more hands-on and practical. Over the last couple of months we wrote a collection of cryptographic building blocks in the Noir programming language, implementing some designs explained in our previous posts. The latest addition to our toolbox is Poseidon (co-authored by one of our co-founders) and Poseidon2, which are the 4th and 5th algorithms we implemented. If you are interested in reading an in-depth analysis of the others, let us know! We might write more posts about them in the future.
In this blog post we provide insights into the implementation of Poseidon, the most commonly used and battle-tested zk-friendly hash function, and an improved version of it, Poseidon2.
Poseidon in Noir
This is not the first blog post about Poseidon (not even the first one focused on Noir). Therefore, we will try to keep the technical intricacies (and the math) to a minimum. Nevertheless, let's start with a brief background for those new to Noir or Poseidon.
Noir
Noir is a zkDSL developed by the folks from Aztec. The syntax and design principles are heavily influenced by Rust. You can read about Noir and its design in detail on their GitHub or Aztec's website, if you are interested. The Noir ecosystem is constantly evolving, first and foremost through the core team's improvement of the language itself and the fast addition of new features. Additionally, a rather large community is already extending the Noir landscape by developing libraries and writing applications with Noir. The awesome Noir repository is a hub for those community-driven projects (where you can also find our crypto libraries 😉).
We will show you some code snippets in this post, so to get you familiar with it, here is a snippet on how to use the Noir standard library to hash 8 Field elements with Poseidon:
use dep::std::hash::poseidon;
fn main(plains: [Field; 8]) -> pub Field {
poseidon::bn254::hash_8(plains)
}
Listing 1: Hashing 8 Field elements with Poseidon in Noir.
This post does not aim to be a Noir tutorial (there are quite a few out there). The rest of the blog post is readable even if you do not know Noir, but it may help though.
A way too short intro to Poseidon
This part of the post will give you a concise overview of the fundamental building blocks and design rationale behind Poseidon. If you're seeking an in-depth exploration of the mathematical intricacies, this post may not delve into the depths you desire. Fear not, though, as alternative resources are available to meet your needs. Additionally, you can read the Poseidon paper on e-print.
If you have read the first two blog posts in the series, you know that Poseidon relies on low-degree round functions. To understand what we mean by that, have a look at this picture:
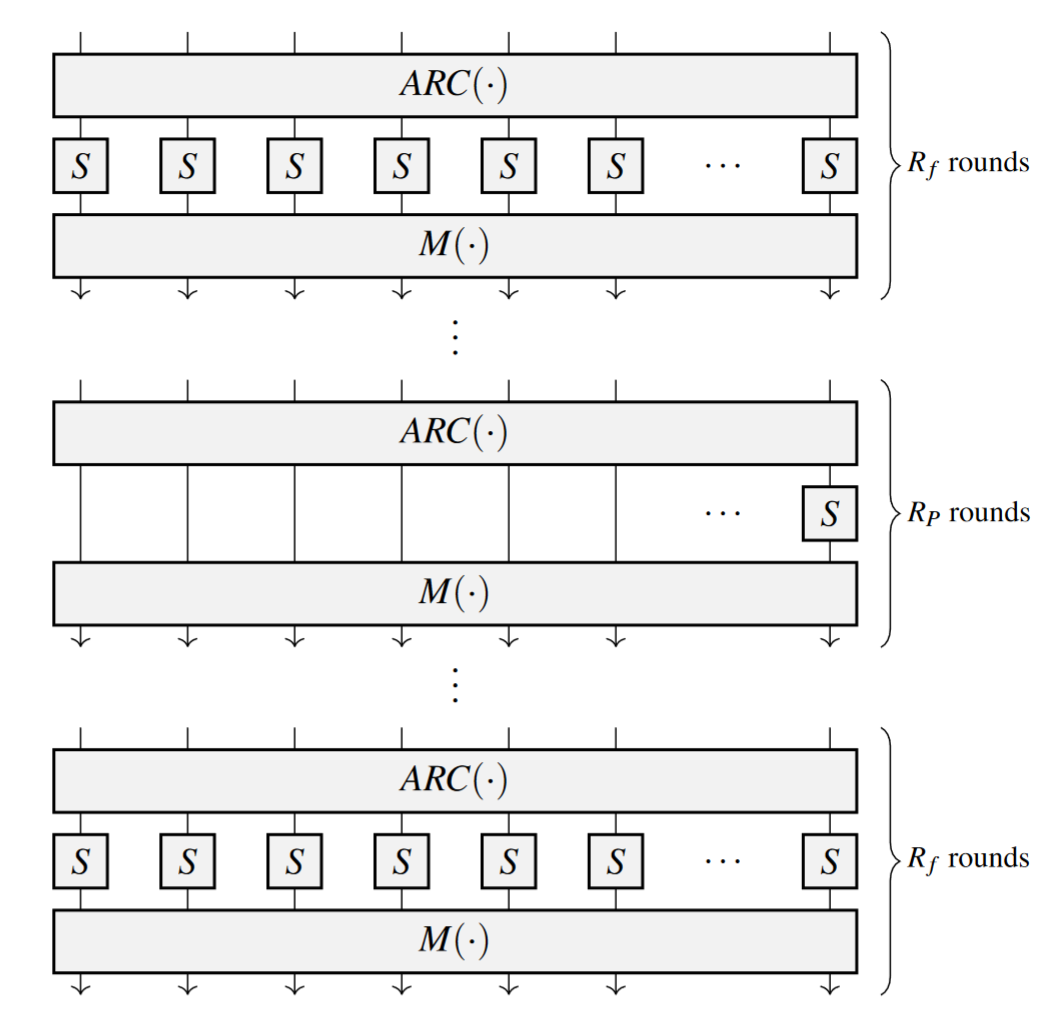
Figure 1: The Poseidon permutation obtained from the Poseidon paper.
The picture depicts the Poseidon permutation. The permutation works on a state size $t$ and is composed by a number of rounds, which are split into full and partial rounds, denoted as $R_f$ and $R_p$ in the picture above. Every round consists of three steps:
- AddRoundConstants - adds pre-defined constant values to the state
- SubWords - a non-linear layer s-box (the low-degree round function)
- MixLayer - a linear layer matrix multiplication with a $t \times t$ MDS matrix
The s-box is a low-degree polynomial in the form $y=x^d$, where $d$ is the degree of the round function. The choice of $d$ usually depends on the underlying field size and is chosen to be the smallest number such that $y=x^d$ is invertible. The full and partial rounds are equivalent in structure except for the non-linear layer. The partial rounds' non-linear layer consists of only 1 s-box and $t-1$ identity functions, whereas in the full rounds, we apply $t$ s-boxes.
When we talk about Poseidon, we usually mean a concrete instantiation of the permutation. The Poseidon paper does give certain restrictions on the choice of the parameters, but is otherwise rather loose about the instantiations. Therefore there is no "official" version of Poseidon (yet). The instantiations that come closest to official, if you want to call it that, are defined by this Sage script linked in the paper, written by one of the authors.
The selection of the 'correct' instantiation, meeting the desired security threshold, is closely tied to the underlying field order of the zero-knowledge proof system. Specifically, for the commonly used scalar fields of the BLS12-381 and BN254 elliptic curves, the paper advises opting for $d=5$ and, for achieving 128-bit security, recommends 8 full rounds and 60 partial rounds with a state size of $t=5$. The paper also provides MDS matrices and round constants generated through the Sage script linked above. Nevertheless, it's essential to note that any other instantiation adhering to the security assumptions outlined in the paper qualifies as a valid configuration for Poseidon.
Improving Poseidon
Now, with the preliminaries out of the way, we can discuss our implementation of Poseidon in Noir. The alert reader may ask: "Why did you rewrite Poseidon when there is already one in the standard library?". That is a fair question and we have two reasons for it. Firstly, we think it is fun to write crypto. Especially in Noir. The second reason is that the folks from Aztec asked us to look into their Poseidon2 implementation and while we were at it, if we could check whether we could improve the already implemented Poseidon.
Therefore, the first step was to investigate the already existing implementation.
pub fn permute<M, N, O>(pos_conf: PoseidonConfig<M, N>, mut state: [Field; O]) -> [Field; O] {
let PoseidonConfig {t, rf: config_rf, rp: config_rp, alpha, ark, mds} = pos_conf;
let rf = 8;
let rp = [56, 57, 56, 60, 60, 63, 64, 63, 60, 66, 60, 65, 70, 60, 64, 68][state.len() - 2];
assert(t == state.len());
assert(rf == config_rf as Field);
assert(rp == config_rp as Field);
let mut count = 0;
// First half of full rounds
for _r in 0..rf / 2 {
for i in 0..state.len() {
state[i] = state[i] + ark[count + i];
} // Shift by round constants
for i in 0..state.len() {
state[i] = state[i].pow_32(alpha);
}
state = apply_matrix(mds, state); // Apply MDS matrix
count = count + t;
}
// Partial rounds
for _r in 0..rp {
for i in 0..state.len() {
state[i] = state[i] + ark[count + i];
} // Shift by round constants
state[0] = state[0].pow_32(alpha);
state = apply_matrix(mds, state); // Apply MDS matrix
count = count + t;
}
// Second half of full rounds
for _r in 0..rf / 2 {
for i in 0..state.len() {
state[i] = state[i] + ark[count + i];
} // Shift by round constants
for i in 0..state.len() {
state[i] = state[i].pow_32(alpha);
}
state = apply_matrix(mds, state); // Apply MDS matrix
count = count + t;
}
state
}
Listing 2: Standard library's Poseidon permutation copied from this GitHub link.
The listing shows the entirety of the Poseidon permutation. You can clearly see the code for the full and partial rounds, with each round executing the three aforementioned steps. The first parameter of the function PoseidonConfig specifies the concrete instantiation, including the degree $d$, the MDS matrix, round constants, state size $t$, and the count of full and partial rounds. Before we continue, it's crucial to emphasize that Noir's native proving system operates on the BN254 curve, and the presented instantiation is implemented with that curve in mind. As the PoseidonConfig struct may be used with other curves than BN254, the code has to add additional checks, whether the instantiation is suitable for the curve.
The interesting part is on line 13, where we can see the amount of partial rounds is tied to the state size. This segment of the code draws inspiration from the Circom implementation of Poseidon. We already mentioned that there is no standardized or official Poseidon instance. Therefore the authors of the standard library's Poseidon implementation opted for compliance with the Circom implementation, which means supporting state sizes $t \in [2, 16]$. It's worth mentioning that Circom utilizes a number of partial rounds rounded up to the nearest integer divisible by the state size $t$. This choice proves advantageous in certain situations depending on the underlying proof system. However, this approach does not have any benefits for Noir and its plonkish-proof system Barretenberg, which serves as the default proof system for Noir.
This insight effortlessly paves one way to improve the standard library’s Poseidon performance. The amount of executed rounds directly correlates with the costs of the implementation. In the context of a plonkish-proof system, such as Barretenberg, these costs are typically illustrated as rows in a trace or the required number of constraints. Therefore, by sacrificing compliance with Circom by reducing the number of rounds to the minimum required for security instead of using the multiples of $t$, we also decrease the necessary constraints for one permutation.
Can we do something else?
OK, we have seen that we can reduce the amount of rounds. What else could we do to achieve better performance? We cannot simply decrease the degree of the round function of the s-box since $d=5$ is already the optimal choice for BN254. So, nothing we can do here.
Let's have a look at the MixLayer, though. Remember, the linear layer is a matrix multiplication with an MDS matrix. The standard library implements that like this:
fn apply_matrix<N, M>(a: [Field; M], x: [Field; N]) -> [Field; N] {
let mut y = x;
for i in 0..x.len() {
y[i] = 0;
for j in 0..x.len() {
y[i] = y[i] + a[x.len()*i + j]* x[j];
}
}
y
}
Listing 3: Standard library's basic matrix multiplication from this GitHub link.
This is a pretty standard matrix multiplication. Maybe we can do something better here?
An MDS matrix has the property that all of its sub-matrices are invertible. This means we can use different matrices for the linear layer, as long as the matrix has these properties. Still, not every MDS matrix provides the same security (as mentioned in the Poseidon paper). So, theoretically, we could find a better MDS matrix where the matrix multiplication is cheaper with the restriction that we do not want to sacrifice security. In fact, this has already been done in related work!
Introducing another zk-friendly hash function that we've already integrated into our toolbox: Griffin! Developed by the same core research team as Poseidon, including two of our co-founders, Griffin stands out as a modern zk-friendly hash function that heavily outperforms Poseidon concerning necessary constraints. The Griffin permutation also uses an MDS matrix for its linear layer, and in contrast to Poseidon the authors specify concrete matrices that shall be used for different state sizes. Unfortunately, Griffin does not allow a choice of arbitrary state sizes. Griffin only supports state sizes $t \in {2, 3, 4, 8, 12, 16, 20, 24}$. Although Griffin allows state sizes $t\in {8,12,16}$ the paper does not introduce MDS matrices for those state sizes, but reuses the $4\times 4$ MDS matrix for the linear layer, a technique that we cannot reuse for Poseidon, but as we will later see, serves as baseline for some matrices in Poseidon2. Therefore we can only reuse the MDS matrices for state sizes $t \in {3,4}$.
Nevertheless, here are the MDS matrices obtained from Griffin:
$$ \text{MDS}_2 = \text{circ}(2\text{ }1) $$
$$ \text{MDS}_3 = \begin{pmatrix} 2 & 1 & 1\\ 1 & 3 & 1\\ 1 & 1 & 2 \end{pmatrix} $$
$$ \text{MDS}_4 = \begin{pmatrix} 5 & 7 & 1 & 3\\ 4 & 6 & 1 & 1\\ 1 & 3 & 5 & 7\\ 1 & 1 & 4 & 6 \end{pmatrix} $$
We snuck in the trivial MDS matrix (not obtained from Griffin) for state size $t=2$ as the circular matrix of $2,1$. OK, and now? Have a look at the implementation of the linear layer for those aforementioned state sizes now:
pub fn mds_2(state: [Field; 2])->[Field; 2] {
let sum = state[0] + state[1];
[sum + state[0], sum + state[1]]
}
fn mds_3(state: [Field; 3])->[Field; 3] {
let sum = state.reduce(|a,b| a + b);
let mut ret_val = [0; 3];
ret_val[0] = state[0] + sum;
ret_val[1] = 2 * state[1] + sum;
ret_val[2] = state[2] + sum;
ret_val
}
pub fn mds_4(mut state: [Field; 4]) -> [Field; 4] {
let t_0 = state[0] + state[1];
let t_1 = state[2] + state[3];
let t_2 = double(state[1]) + t_1;
let t_3 = double(state[3]) + t_0;
let t_4 = double(double(t_1)) + t_3;
let t_5 = double(double(t_0)) + t_2;
state[0] = t_3 + t_5;
state[1] = t_5;
state[2] = t_2 + t_4;
state[3] = t_4;
state
}
Listing 4: The streamlined matrix multiplications for state sizes $t \in {2,3,4}$.
Given that the MDS matrices primarily consist of ones, a streamlined approach to matrix multiplication becomes feasible. Furthermore, leveraging the observation that the remaining elements are generally small reduces the number of required multiplications. This optimization proves advantageous, both for native hashing and ZK performance, considering that multiplications are more costly than additions in zk.
About MDS matrices and round constants
Excellent, we managed to find better MDS matrices for state sizes $t \in {2, 3, 4}$. That is great, but what about the rest of the pack? Recall that the standard library's Poseidon implementation accommodates a state size up to $t=16$. Once again, we can capitalize on the contributions of our co-founders, who co-authored this paper! In the paper, the authors provide improvements for the linear layer for LowMC, which is an ancestor of Poseidon (Poseidon is actually a variant of HadesMiMC).
In fact, the paper introducing the Hades design strategy applies the same technique for HadesMiMC, and, therefore Poseidon!
Both improvements lower the computational and space complexity of the partial rounds. In contrast to the other two optimizations we identified so far, this optimization is an equivalent transformation of the permutation. When reducing the amount of partial rounds or changing the MDS matrices, we get new instantiations of Poseidon, which means they are not compatible with the old version. The optimization we explain throughout the next paragraphs could theoretically be applied on the standard libraries version as well, while remaining compatible with the old implementation!
OK, remember, we cannot change the low-degree round function, but the AddRoundConstants and the MixLayer are fair game (given that we do not compromise security). So, let's look into what the paper proposes for those two layers. The explanation in the upcoming paragraphs summarizes the paper's findings, but we encourage you to read the paper for a more in-depth explanation.
AddRoundConstants
For Substitution-Permutation-Networks (SPN) that use partial non-linear layers in $R_p$, like Poseidon, swapping the linear layer and the round constant addition is possible, as both operations are linear and are not transformed by a non-linear function in between. Remember, during the partial rounds we only apply the non-linear (the s-box) layer to a single state element, while the other state elements remain.
Poseidon is a good candidate for this, because its partial non-linear layer is pretty small (only 1 s-box) and it has a relatively high amount of partial rounds, which all benefit from this transformation. When doing this, the round constants need to be exchanged with equivalent ones, whereas the equivalent ones can be computed as $\hat{rc}^{(i)} = \text{MixLayer}^{-1} (rc^{(i)})$.
When dealing with partial rounds—where a single s-box and $t−1$ identity functions come into play—we can leverage this observation to strategically shift portions of the round constants 'through' these partial rounds. By applying this process to all partial rounds, we effectively transfer all round constants to an 'earlier round,' signifying that the addition of round constant $rc$ is now relocated to the previous round. In this preceding round, the transformed round constant undergoes a split into two parts: the values destined for addition to the s-box element, and the remainder. The first part is seamlessly integrated into the s-box element while the other portion undergoes a further upward shift in the process.
Finally, after the round constants from the first partial round have been shifted to the previous round, we obtain a "0th round", consisting of a single addition of all the condensed round constants, executed after the full rounds. This approach saves us $(t-1)\cdot R_p - 1$ additions!
MixLayer
The paper uses a similar approach for the MixLayer. OK, we lied at the beginning of the blog post; there will be math in this section, but it is not too complicated. Again, focusing on the partial rounds, let $M$ be the $t\times t$ MDS matrix, we can write $M$ as:
$$ M = \begin{pmatrix} M_{0,0} & v \\ w & \hat{M} \\ \end{pmatrix} $$
where $\hat{M}$ is a $(t-1)\times(t-1)$ MDS matrix (recall, by definition every sub-matrix of an MDS matrix is also MDS), $v$ and $w$ are vectors of length $t-1$ and $M_{0,0}$ is a scalar. Further, the paper states:
$$ M = \underbrace{\begin{pmatrix} 1 & 0 \\ 0 & \hat{M} \end{pmatrix}}_{M^{\prime}} \times \underbrace{\begin{pmatrix} M_{0,0} & v \\ \hat{w} & I \end{pmatrix}}_{M^{\prime\prime}} $$
where
$$ \hat{w} = \hat{M}^{-1} \times w $$
and $I$ is the $(t-1)\times(t-1)$ identity matrix. Similar to the approach used during the AddRoundConstants step, we can move the matrix multiplication with the matrix $M^\prime$ to the prior rounds. Additionally, the matrix multiplication that "stays" in the round is a multiplication with the matrix $M^{\prime\prime}$, which is a sparse matrix. This means that we can save a lot of multiplications!
In code this looks like:
fn permute_bn254<T, RP, T1>(mut state: [Field; T], config: PoseidonBn254Config<T, RP, T1>) -> [Field; T] {
for i in 0..4 {
state = hash_utils::vec_add(state, config.first_full_rc[i]);
state = poseidon::sbox(state);
state = hash_utils::mat_mul(state, config.mds);
}
//the 0-th round
state = hash_utils::vec_add(state, config.opt_rc_outer);
state = hash_utils::mat_mul(state, config.m_i);
for r in 0..RP {
state[0] = poseidon::sbox_e(state[0]);
//only one addition for round constant
state[0] = state[0] + config.opt_partial_rc[r];
//the cheaper mat mul with M^\prime\prime
state = cheap_matmul(state, config.v[RP - r -1], config.w_hat[RP - r -1], config.mds[0][0]);
}
for r in 0..4 {
state = hash_utils::vec_add(state, config.second_full_rc[r]);
state = poseidon::sbox(state);
state = hash_utils::mat_mul(state, config.mds);
}
state
}
Listing 5: The optimized Poseidon permutation for state sizes $t \in [5, 16]$.
The aforementioned transformations become evident upon closer examination. Following the initial four full rounds, we add the accumulated round constants to the state, which "ascended upward" through the partial rounds. After that, we perform a matrix multiplication with the condensed matrices from the linear layer. Subsequently, we proceed with the partial rounds. As elucidated earlier, in the implementation, a round constant is exclusively added to the singular state element transformed by the s-box. In contrast, all other round constant additions are placed before the loop.
The last thing we need to do is to perform the matrix multiplication of the state with $M^{\prime\prime}$. Remember, $M^{\prime\prime}$ is a sparse matrix of the form:
$$ M^{\prime\prime} = \begin{pmatrix} M_{0,0} & v \\ \hat{w} & I\\ \end{pmatrix} $$
so we can again save a lot of multiplications. You can see the cheap_matmul function here:
fn cheap_matmul<T, T1>(mut state: [Field; T], v: [Field; T1], w_hat: [Field; T1], mds: Field) -> [Field; T] {
let mut new_state = [0; T];
new_state[0] = mds * state[0];
for i in 0..T1 {
new_state[0] += w_hat[i] * state[i+1];
}
for i in 1..T {
new_state[i] = state[0] * v[i-1] + state[i];
}
new_state
}
Listing 6: The optimized matrix multiplication with $M^{\prime\prime}$.
Remember that $v$ and $\hat{w}$ are $(t-1)$ length vectors, so we have to perform two dot products of length $t-1$. Additionally, at the start of function we have to do a single multiplication with the scalar $M_{0,0}$. This means instead of $t$ dot products of size $t$, we only have to perform 2 dot products of size $(t-1)$ and one multiplication! This is a huge improvement, especially for larger state sizes.
Poseidon2
This is as far as we can get with the Poseidon permutation. Luckily, there is a faster variant of Poseidon, Poseidon2 (easy to memorize, right?).
Poseidon2 improves on specific needs that arose during the usage of Poseidon in the real world. One common use case is the computation of large Merkle trees. A problem with designs like Poseidon is that they are optimized with the complexity of their arithmetic circuit in mind. This often leads to a rather lousy performance on traditional CPUs which is still relevant when having to compute a large Merkle tree. If you are interested in this topic, we recommend reading the second blog post of this series.
There was no implementation of Poseidon2 in Noir, so we could just start from scratch. First of all, Poseidon2 is really an optimized version of Poseidon. This becomes clear when comparing the two permutations:
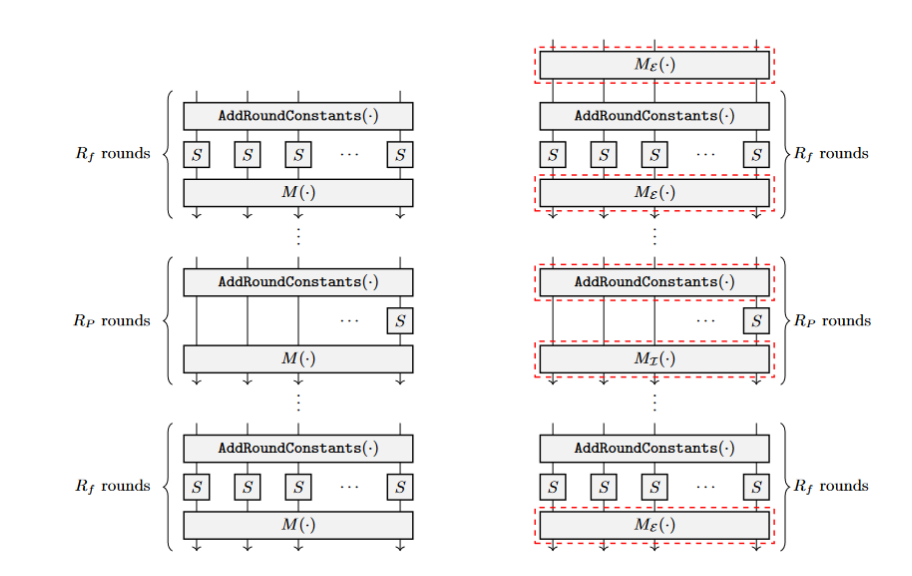
Figure 2: comparison of Poseidon and Poseidon2, obtained from the Poseidon2 paper (the permutation on the right being Poseidon2).
The figure shows that Poseidon2 still uses the same three layers per round and also has a set of full and partial rounds. However, the Poseidon2 permutation uses two different linear layers for the full and partial rounds. Additionally, Poseidon2 has one additional full linear layer before the first full round. This addresses a property of Poseidon that was pointed out in third party cryptanalysis 1.
Here is the code for our Noir Poseidon2 permutation:
fn permute_bn254<T, R>(mut state: [Field; T], mm_external: fn([Field; T]) -> [Field; T],
mm_internal: fn([Field; T]) -> [Field; T], config: Poseidon2Bn254Config<T,R>) -> [Field; T] {
state = mm_external(state);
for r in 0..4 {
state = hash_utils::vec_add(state, config.first_full_rc[r]);
state = poseidon::sbox(state);
state = mm_external(state);
}
for r in 0..R {
state[0] += config.partial_rc[r];
state[0] = poseidon::sbox_e(state[0]);
state = mm_internal(state);
}
for r in 0..4 {
state = hash_utils::vec_add(state, config.second_full_rc[r]);
state = poseidon::sbox(state);
state = mm_external(state);
}
state
}
Listing 7: The Poseidon2 permutation.
Funny enough, the most complicated part of the code snippet is the function declaration. The permutation itself is pretty straightforward, and one can easily see the structure of the permutation as described above.
The two parameters mm_external and mm_internal are function pointers to the implementation of the respective linear layers. The authors specify that for the Poseidon2 permutation it is NOT necessary to use MDS matrices. Another performance improvement is that the internal matrices have 1s everywhere except in the main diagonal. To give an example, look at the matrices for state size $t=3$:
$$ M_{\mathcal{I}} = \begin{pmatrix} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 3\end{pmatrix} $$
$$ M_{\mathcal{E}} = \begin{pmatrix} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2 \end{pmatrix} $$
With these matrices we can again streamline the matrix multiplication:
fn internal_3(state: [Field; 3])->[Field; 3] {
let sum = state.reduce(|a,b| a + b);
let mut ret_val = [0; 3];
ret_val[0] = state[0] + sum;
ret_val[1] = state[1] + sum;
ret_val[2] = 2 * state[2] + sum;
ret_val
}
fn external_3(mut state: [Field; 3])->[Field; 3] {
let sum = state.reduce(|a,b| a + b);
state[0] += sum;
state[1] += sum;
state[2] += sum;
state
}
Listing 8: The streamlined matrix multiplications for state size $t=3$.
Poseidon2, similar to Griffin, has a limited set of state sizes. In fact, the reason for that is that they use the same approach for designing the external linear layers. Poseidon2 allows state sizes $t\in {2,3,4t^\prime,\dots, 24} \text{ for } t^\prime \in \mathbb{N}$. As the Noir standard library supports Poseidon up to state size 16, we also implemented all the possible state sizes up to $t=16$. For brevity (and because this post is already really long), we do not discuss the implementations for the other matrix multiplications in this blog post. You can find the implementations on our GitHub, though.
Putting it all together
Truth be told, this post has turned out to be a bit longer than anticipated. We intended to delve into the evolution of Poseidon and its predecessors. We also wanted to touch on some real world use-cases that already use Poseidon in practice. So consider this a teaser, as there may be a follow-up post to cover this topics in more detail!
But back to the topic at hand, we showed you how we can improve the performance of Noir's Poseidon implementation. To summarize, we:
- Sacrificed compatibility with Circom to reduce the amount of partial rounds.
- Used better MDS matrices for state sizes $t \in {2,3,4}$.
- Used the improvements from this paper to reduce the amount of additions and multiplications of the AddRoundConstants and MixLayer for the other state sizes.
We additionally implemented Poseidon2 in Noir from scratch.
Now, of course, we want to compare the three implementations. Luckily, Noir has one easy way to estimate the cost of zk circuits. This works with Noir’s package manager, Nargo. Nargo can count the necessary constraints of a Noir circuit to compare the constraints required for the two implementations. Of course, other ways to compare those implementations are also important (plain performance for filling the trace, necessary space, …), but the circuit size is the easiest to see and verify!
So, here are the results:
| # | Poseidon (stdlib) | Poseidon | Poseidon2 |
|---|---|---|---|
| 2 | 586 | 586 | 586 |
| 3 | 2183 | 2098 | 2094 |
| 4 | 2353 | 2305 | 2313 |
| 5 | 2833 | 2507 | - |
| 6 | 3059 | 2795 | - |
| 7 | 3532 | 3031 | - |
| 8 | 3877 | 3283 | 3139 |
| 9 | 4076 | 3551 | - |
| 10 | 4123 | 3835 | - |
| 11 | 4948 | 4135 | - |
| 12 | 4751 | 4451 | 3995 |
| 13 | 5539 | 4783 | - |
| 14 | 6388 | 5131 | - |
| 15 | 5813 | 5495 | - |
| 16 | 6581 | 5875 | 4883 |
Table 1: The constraints for the different implementations. Every cell represents the amount of constraints for a single run of the permutation
As evident, our Poseidon implementation surpasses the current standard library across all state sizes, except for size 2, where performance remains consistent across all three implementations. Nevertheless, as anticipated, the improvements only get more pronounced as the state size grows!
Poseidon2 is also the same for state size $t=2$. Interestingly, for state size $t=4$ Poseidon2 has a slightly higher number of constraints. Still, it considerably outperforms the other two implementations for all other state sizes. Additionally, remember that this comparison is incomplete as we just compare the plonkish constraints. The main advantage of Poseidon2 is its way faster plain performance, which is not shown by this table at all.
We finally made it! This is the end of this post. We hope you enjoyed it and maybe also learned something while reading! Watch out for the upcoming blog posts, there are a few more about zk-friendly hashing in the pipeline! There is also another one with a slightly different topic on the horizon ;)
The property is described in this paper if you are interested. It addresses SPNs in sponge mode, like Poseidon and Poseidon2.