Private Proof Markets using MPC

As much as we like to talk about Zero Knowledge, especially zk-friendly hash functions, we also enjoy to talk about other privacy-enhancing technologies (PETs). ZK is for sure the standout PETs performer in web3 today, with homomorphic encryption (HE) taking a little bit of spotlight as well. A technology that does not (yet) get as much spotlight as the other two is Multiparty Computation (MPC) and we want to change that! In this post we outline ideas on how to combine ZK and MPC (often dubbed Collaborative SNARKs ¹) and discuss the technical feasibility of such a framework. Additionally, we explain a potential use case of Collaborative SNARKs discussing how to enhance the privacy of ZK proof markets, using the example of =nil; foundation's proof market!

Proof Markets

Before we dive into the nitty-gritty details of Collaborative SNARKs, we will start with something lightweight. In our case example, we work on =nil; foundation's proof market, so let's explore the concept and technology of such proof markets. Imagine you want to create a ZK proof for your computation. However, your computation is comparably large and you lack the computational resources to create the proof yourself. Indeed, proving any program with modern ZK provers induces a huge computational overhead, alongside large RAM requirements. Proof markets are a solution to your problem: They allow users to outsource proof generation to provers who monetize their more powerful hardware, which potentially also includes accelerators optimized for ZK.

Proof markets create a mutually beneficial scenario for both buyers and sellers. Sellers earn money by utilizing optimized hardware for efficient proof creation, providing buyers with cost-effective proofs. However, in today's real-world scenario, provers often have to disclose potentially sensitive information to the proof producer. To understand the concerns, let's first inspect how a ZK proof is generated.

ZK Proof Generation

On a high-level, a ZK proof allows a prover to convince a verifier that it knows a witness $w$ attesting to the validity of a NP relation $\mathcal{R}$ without revealing anything about the witness (except what can be derived from the relation $\mathcal{R}$ itself). In many cases we are concerned with proving that a computation (represented by a circuit $C$) was performed correctly on an input $x$, producing a output $y = C(x)$. In other words, the (potentially) private input $x$ serves as the witness of the ZK proof and the NP relation is encoded as a circuit $C$ which uniquely connects $x$ to the (potentially public) output $y$.

In modern ZK proving systems, a proof is generated in two steps. First, the circuit is encoded into a representation understood by the proof system, which nowadays usually either means representing it as a set of R1CS constraints or polynomial constraints for Plonkish proof systems. This representation only depends on the circuit $C$ and is actually independent of the input $x$. The next step is assigning the circuit, i.e., evaluating it on the input $x$. Thereby, we also have to remember all intermediate values which are part of the circuit-representation constraints, since these are also required during proof generation. We now call the combination of $x$ and the intermediate values the extended witness $t$.

The role of the ZK proof system is then to take the circuit representation, as well as the assignments $t$ as input and create a valid ZK proof.

Outsourced Proof Generation

OK, let's get back to the outsourcing of ZK proof generation to proof markets. To outsource a proof, a user needs to outsource a circuit that can be represented as a set of constraints understood by the proof system, as well as the circuit assignment containing the extended witness. In a more general setting, the user could also just outsource the input $x$ instead of the assignment and let the prover also create the extended witness. In both cases though, the input $x$ is send from the user to the prover, either directly, or as part of the extended witness.

In use cases where $x$ is not considered to be private (for example when only the succinctness property of modern ZK proof systems is required and not the zero-knowledge property itself), this approach does not invade privacy. However, when the witness $x$ contains private information, the user may not be willing to give it to the prover. Indeed, in an open proof market environment, potential competitors could pose as provers and try to steal private information.

To summarize, if you want to create a ZK proof, you nowadays have two options. First, you create it on your own, potentially requiring vast computational and RAM resources, but fully preserving privacy (see Figure 1, left image). Second, you can use a proof market where you outsource proof generation in exchange for a fee, trading away your potentially private inputs in exchange for requiring less powerful hardware (see Figure 1, right image).

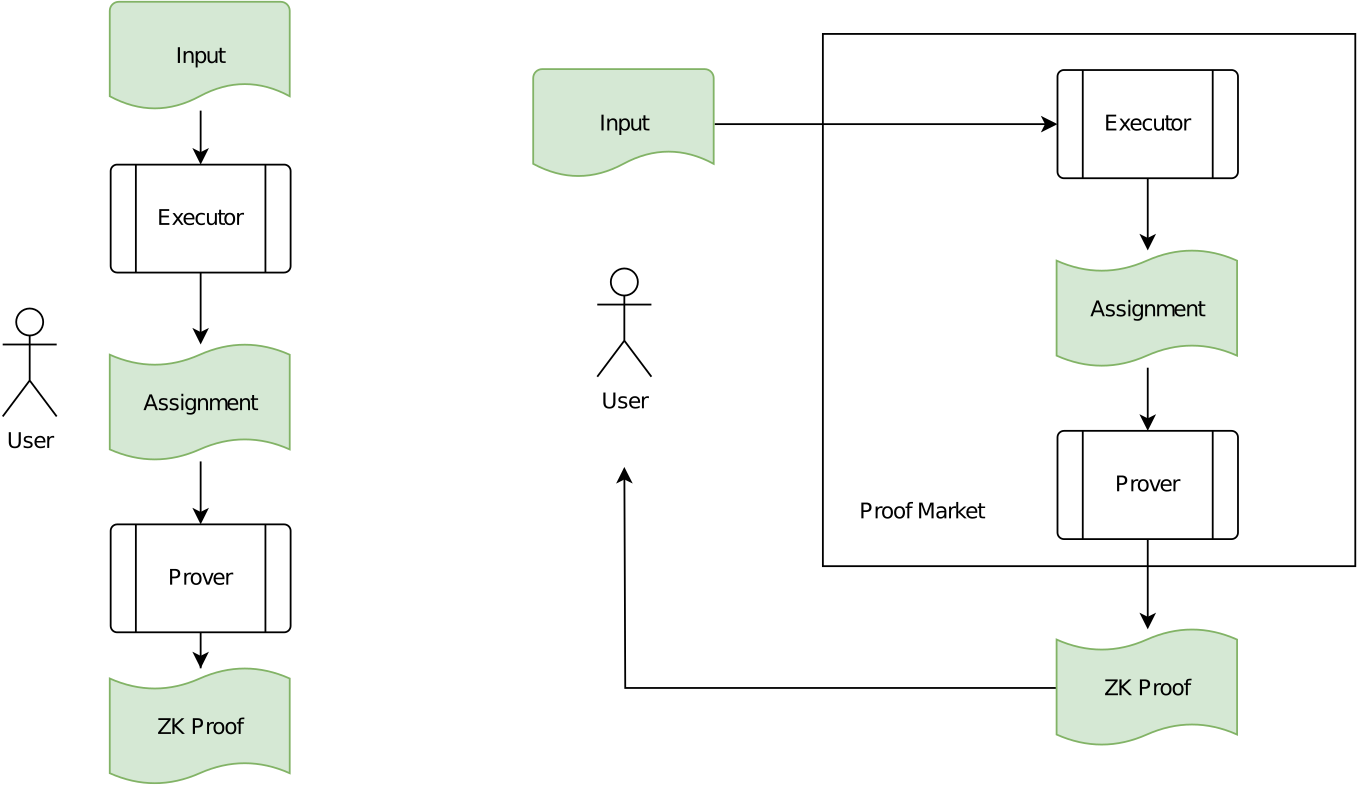
Figure 1: Local proof generation (full privacy) on the left compared to a proof market (no privacy) on the right.

The Solution: MPC

To understand how MPC can solve this problem, it is necessary to get some background about MPC. Let's start with the description usually used in the literature:

MPC is a subfield of cryptography that enables multiple parties to jointly compute a function $f$ over their combined inputs, while keeping these inputs private.

OK, let's dissect that information. Similar to ZK, the evaluated function $f$ is usually represented as an arithmetic circuit. The inputs to $f$ are secret-shared² among the parties. Every party evaluates the circuit locally on their shares and communicates with the other participants when necessary. After the parties finish their computation, they reconstruct the result of the function $f$ without ever telling anyone the secret inputs. In practice, the parties computing the function are not necessarily the same parties that provided the inputs. We can use this property to enable privacy for outsourced computations, such as proof markets!

The workflow is as follows: A user, instead of sending the (extended) witness to one prover who then produces the proof, secret-shares it to a set of $n$ provers. Thereby, due to secret sharing, an individual prover does not get any information about the (extended) witness, but all provers together can use MPC to create a valid zero knowledge proof.

We depict the case where the extended witness is created by the user in Figure 2. Since MPC allows to compute any function, creating the extended witness can potentially also be outsourced to the proof market.

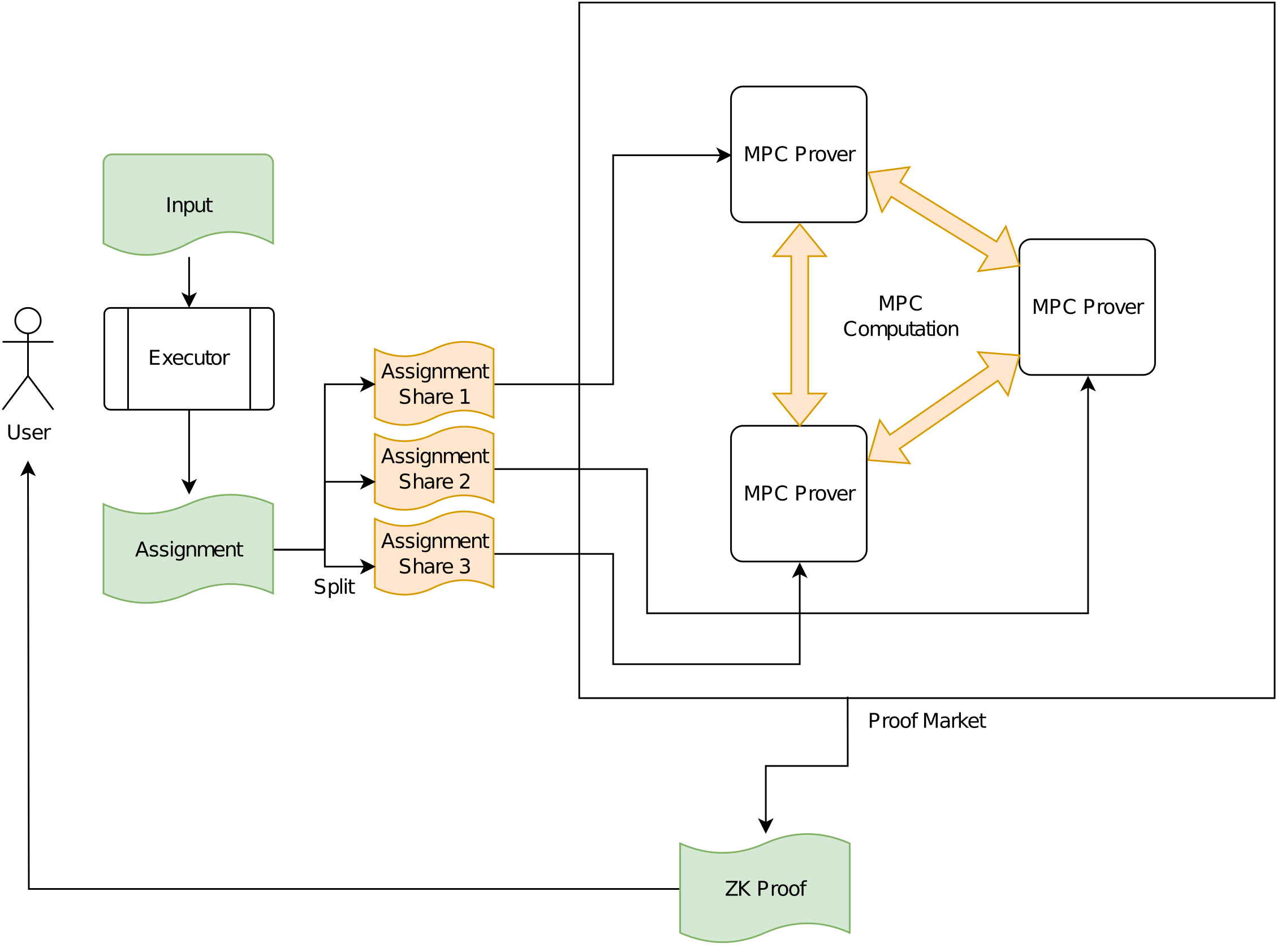
Figure 2: Collaborative Proof Market using MPC (full privacy).

So this solution requires to create the ZK proof inside an MPC protocol. Similar to ZK, using MPC usually adds a significant performance penalty to the evaluation of any function. This begs the question: Can such a solution even be efficient enough for practical use?

Efficiency of MPC-Based Proof Generation

Secret-sharing based MPC protocols usually have two factors where they add overhead to computing a function. First, and foremost, for each non-linear operation (e.g., multiplying two shared values) the computing parties need to exchange randomized data. Hence, evaluating a function with tons of multiplications leads to gigabytes of data being exchanged between the computing parties. This communication can easily become the bottleneck in many MPC applications, especially in slow network environments. Hence, functions with a small number of multiplication are preferred.

Second, without wanting to go into too much details, some MPC protocols require extra computational effort compared to just evaluating the function. In replicated sharing protocols (e.g., ABY3) and SPDZ-like protocols, each party has to perform the computation on multiple shares, increasing workload. Furthermore, many MPC protocols, similar to ZK proving systems, operate over larger prime fields, which have some overhead when evaluating circuits which are not defined over these fields.

So how are ZK proving protocols faring with these limitations in mind? Since ZK proving systems usually operate over large prime fields, no overhead is to be expected from using an MPC protocol defined over the same fields. The more sever question, however, concerns the number of multiplications required for generating the proof, which in turn defines the required communication between the MPC parties. The answer, unfortunately, depends on the type of ZK prove system, more concretely, the used polynomial commitment scheme.

KZG and IPA

For proof systems build form the popular KZG commitment scheme, or from inner product arguments (IPA) such as Halo2, the main steps involve Fast Fourier Transforms (FFTs), multi-scalar multiplications of the form $\sum_i s_i G_i$ where $G_i$ is a point on an elliptic curve, and dividing polynomials by $(X-x)$ for a publicly known $x$.

Since linear operations, such as additions and multiplying secret values by publicly known ones, do not require communication between the MPC parties, all of these mentioned steps can be computed without the parties having to communicate with each other. Indeed, the FFT is known to be a linear operation which can be represented by a matrix-vector multiplication where the matrix is public, the generators $G_i$ for the multi-scalar products are usually public, and dividing by $(X-x)$ for a public $x$ boils down to linear operations as well. Consequently, the computationally most expensive parts of the proof generation can be computed locally by the computing parties and do not require interactions. Even better: Since secret shares of field elements are also field elements, and linear operations on shares usually being equivalent to the non-MPC counterpart, most operations in these proof systems do not differ from standard proof generation. Consequently, special proof-generating hardware accelerators can crucially be used in combination with MPC as well. Thus, KZG and IPA based proof systems are very well suited for MPC-based proof markets.

FRI

Unfortunately, the same cannot be said about FRI-based proof systems. FRI extensively relies on cryptographic hash functions to construct large Merkle trees during proof generation. In contrast to proofs based on KZG, where hash functions are only applied to public inputs for the Fiat-Shamir transform, FRI requires hashing of secret data. Consequently, when using MPC, these hash functions must be evaluated within the MPC protocol. Traditional hash functions, such as SHA-256, which involve a significant number of multiplications, are not well-suited for MPC evaluation. This challenge bears similarity to hash functions in ZK; for further insights, you can explore our blog post where we delve into more details on this topic.

However, two potential solutions come to mind for this issue in FRI-based proof systems. Firstly, given that ZK-friendly hash functions typically minimize the number of multiplications, one could consider replacing the hash function with a ZK-friendly alternative. This substitution would help limit the communication required between the computing parties. This, however, comes at the cost of larger computational overhead, since ZK-friendly hash functions are usually significantly slower compared to SHA-256. Furthermore, while communication is smaller compared to using SHA-256, one still has to evaluate a huge number of hash functions in MPC leading to a significant communicational overhead compared to KZG-based proofs. A second solution would be to build Merkle-trees on secret-shares instead of concrete values. Thereby, each party computes its own tree locally and no communication is required. As a consequence, $n$ trees (for $n$ parties) are now part of the ZK proof, leading to a blowup of a factor $n$ in proof size. Furthermore, a verifier now has to open $n$ Merkle-trees during proof verification, leading to increased verifier work. While the combination of the $n$ openings is equivalent to the opening in the non-MPC setting, another drawback is that having $n$ Merkle-trees makes the MPC solution incompatible with the unmodified proof system. We will explore the feasibility of these two approaches in the future, but we expect more research is needed for practical applications.

MPC Assumptions and Limitations

So, MPC seems to be a viable option for preserving privacy of witnesses when using proof markets. However, one has to be careful in choosing the right MPC protocol to achieve the desired security guarantees. First, one usually distinguishes between semi-honest and maliciously secure MPC protocols. While semi-honest protocols are significantly more performant compared to malicious variants, they are only secure as long as no party deviates from the protocol. Malicious variants, on the other hand, detect malicious behavior. Further distinctions which affect the choice of protocols, and in turn performance, are the number of computing parties, as well as the number of tolerated malicious parties. While there exist special 3-party protocols (such as the ABY3 line of protocols) which are significantly faster compared to their $n$-party counterparts, they usually require a honest-majority security assumptions, i.e., only 1-out-of-3 parties is allowed to be corrupted. Furthermore, $n$-party honest-majority protocols (e.g., ones based on Shamir's secret sharing) are faster compared to $n$-party dishonest-majority protocols (such as SPDZ), in which only one honest party is required to keep the security guarantees. While this flexibility allows to construct proof markets with different prices for different security guarantees, one needs to carefully consider the choices for the desired use case.

Another factor to consider is the prevention of collusion among the computing parties. Since inputs are secret-shared among the MPC provers, the loss of all privacy occurs if a sufficient number of computing parties collude. In a decentralized proof market, proof producers are not known in advance, necessitating dynamic selection of parties. However, this dynamic selection process introduces the risk of game-theoretic attacks. In such attacks, a colluding group of proof producers may aim to be chosen for the MPC protocol and subsequently attempt to recover the secret inputs. Conventional strategies for selecting parties, such as choosing those with the lowest bids, can enable such attacks, as colluding parties may strategically place very low bids to increase their chances of being selected. Therefore, the selection of the parties needs to be done in a way that is resistant to such attacks. Strategies to mitigate such attacks include selecting parties based on their reputation, adding random parties to the protocol even though they would not have been selected normally or even having a pool of semi-trusted parties that are provided by the proof market itself.

To summarize, we envision three different modes of operation for a proof market to offer high flexibility to users: (i) privacy is not a concern, a single party is chosen to generate the proof, (ii) privacy is a concern, but the user is willing to use a honest majority MPC protocol for performance/cost reasons and (iii) privacy is a concern and the user is choosing a large number of parties that work together in a dishonest majority MPC protocol to gain maximal privacy assurances.

Other Solutions

Since MPC and ZK are only two out of many privacy enhancing technologies out in the wild, we now want to discuss why MPC is, in our opinion, superior for the proof market use case compared to using homomorphic encryption (HE) and trusted execution environments (TEE).

Trusted Execution Environments

Let us start with TEEs. Using a TEE (such as Intel SGX od AMD SEV), a user can encrypt its input for a TEE on a more powerful server. After sending the encrypted data to the TEE, it proceeds with decrypting the data and computing the proof without (explicitly) leaking information to the server. Furthermore, the TEE attests to computing the correct function, increasing trust in the system. However, a TEE-based solution has some severe drawbacks, namely they are highly vulnerable to all kinds of software and physical attacks, such as side channel attacks based on cache timings and power consumption observations with new vulnerabilities and attacks being published on a regular basis³. Since users would give their witnesses to TEEs entirely controlled by potentially malicious parties, these parties could apply these attacks repeatedly to infringe the privacy of the witnesses.

Another point to consider is that using TEEs makes it more difficult to use dedicated ZK hardware accelerators. First, a secure channel needs to be established between the TEE and the accelerator in order to prevent witnesses from leaking during the data transfer. Second, hardware accelerators must be designed to protect the data as well while not allowing debug access to any input data.

Another crucial consideration is that when solely relying on TEEs, trust assumptions become concentrated on a single point, i.e., the TEE vendor. While this may not pose an immediate issue, it presents a shift from decentralized cryptographic primitives to reliance on a centralized hardware manufacturer.

Homomorphic Encryption

Now let's investigate how a different cryptographic solution, namely homomorphic encryption (HE), would fare in combination with proof markets. HE, on first inspection, seems to be a perfect match for outsourcing computations, since its promise on computing any function on ciphertexts allows to replace MPC in our description above, while not requiring multiple computing parties. On closer inspection though, HE also falls short: Today's HE schemes still suffer from huge performance penalties. Since performance of HE schemes without efficient bootstrapping procedure suffers from large multiplicative depths (such as encountered when creating a ZK proof on encrypted data), one inherently has to pick bootstrapping friendly schemes to limit the already huge performance overhead inherent in all HE schemes. However, these schemes come with different problems, namely a small plaintext space. Thus, to mimic operations in larger prime fields, as required for the ZK proof systems, one has to evaluate biginteger circuits on multiple ciphertexts, leading to further slowdown. When using ZAMAs TFHE variant as baseline which requires in the order of 100ms for a single 16-bit multiplication (see benchmarks), one can observe that evaluating a ZK proof on HE encrypted data becomes infeasible very quickly. Finally, many linear building blocks, such as FFTs, can be considered free in MPC, due to not requiring parties to communicate with each other and the local MPC operations being similar to the non-MPC counterparts. In HE, on the other hand, linear operations incur a significant performance overhead as well.

Conclusion

Alright, that's enough of the technical details. We hope we could give you a good overview of why we are excited about combining ZK and MPC. Of course, this blog post only scratches the surface of what is possible with Collaborative SNARKs. Unfortunately, whereas the research output in ZK over the last years increased heavily, the research in Collaborative SNARKs is still in its infancy. Still, there are some interesting papers out there:

• The original Collaborative SNARKs paper
• EOS: efficient private delegation of zkSNARK provers
• zkSaaS: Zero Knowledge SNARKs as a service
• Scalable Collaborative zk-SNARK: Fully Distributed Proof Generation and Malicious Security

This list is by no means exhaustive, but should give you a good starting point to dive into the topic.

For TACEO, we're currently delving deeper into the practical feasibility of Collaborative SNARKs. In addition to the building blocks discussed in this blog post, we're exploring ways to facilitate developers in building Collaborative SNARKs, similar to the advancements made in the ZK space and its DSLs. We're also investigating potential improvements we know for ZK proof systems, such as the cost of lookup arguments in the MPC setting and the applicability of folding techniques. Stay tuned for more blog posts on this exciting topic!