Max Pick Challenge – Part 2

Today is July 15th, which marks the end of our Max Pick Challenge! A big thank you to all participants for your guesses and congratulations to our (anonymous) winner, 0x381f35f3817eee7eee571e5002db13c66e69971f, who snagged a prize of $994 paid out in ETH! We hope you enjoyed the challenge as much as we did and maybe even learned a bit about coSNARKs (collaborative SNARKs) along the way. If you have no idea what we're talking about, you can catch up on the challenge here.

As promised in the previous post, we'll dive into the technical details of the challenge, how we used coSNARKs to compute on private shared state, and what we learned during the process in this post!

From coCircom to dApps

Before we dive into the technical details, let’s take a step back and discuss why we created this demo. Our goal was to demonstrate the feasibility of creating a dApp that can utilize private shared state, allowing multiple parties to compute on their private data without revealing any information to each other.

To achieve this, we've been working on a project that enables developers to build generic coSNARKs—something that wasn’t possible until now. We know that zero-knowledge proofs (ZK) are already challenging. Adding the complexity of Multi-Party Computation (MPC) on top of that makes it even harder. (Can you see where the name of the challenge comes from? 😉) Therefore, we aimed to abstract the MPC part away from the developers and provide them with a tool they already know.

Additionally, we wanted to avoid the need for developers to learn yet another DSL (Domain-Specific Language) or deal with semi-functional transpilers from existing languages like C. Therefore, we chose to use circom, a well-known and widely adopted DSL that comes with rich tooling and a large set of existing circuits. With this in mind, we built coCircom, a tool that allows developers to build coSNARKs using circom (here are the docs).

We released version 0.2.1 a few days ago, and with this version, we created the Max Pick Challenge!

The Challenge

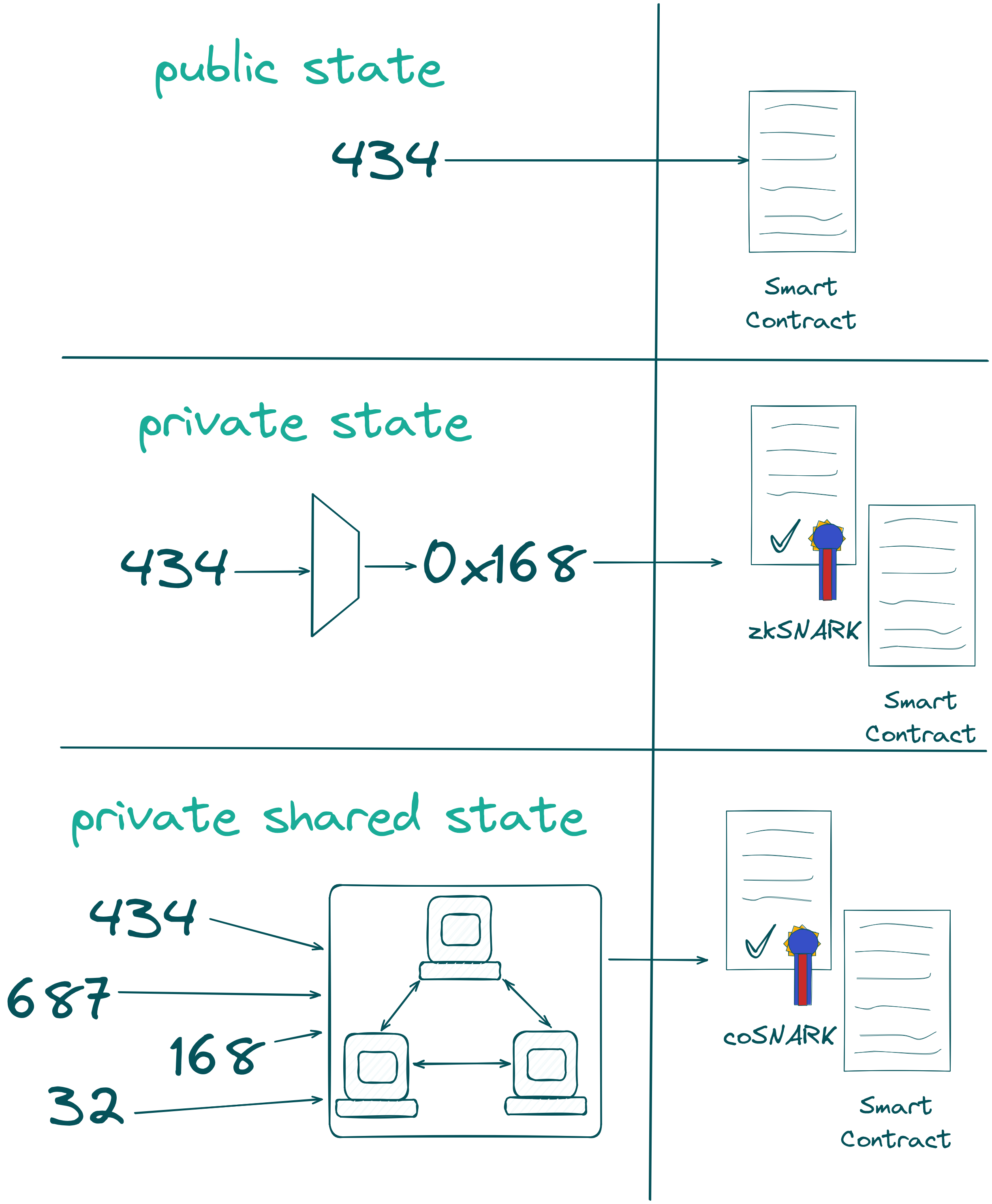
The challenge itself was simple: guess the maximum unique value $x$ in the range $x \in [1,1000]$. Emphasis on unique—if someone else already guessed the same number, both your guesses would be invalid. The winner gets the ETH value equivalent to $x$ dollars. You can see why the traditional public state of blockchains is not feasible in this scenario. We need to ensure that no one can see the guesses of other players. Otherwise, it would be easy to just pick the highest unique number, reducing the game to a matter of timing. Additionally, it would be simple to invalidate others' guesses by picking the same number.

We could try to use private state on privacy-first blockchains like Aztec and Aleo, but verifying uniqueness would require revealing all participants' guesses or sending them to a trusted third-party. This is clearly undesirable for many applications. This is where coSNARKs and private shared state come in. We can use them to verify the uniqueness of the guesses without revealing them.

What happens if you submit a guess?

If you recall from our first blog post, we mentioned that there are four different actors in the Max Pick Challenge. Let's go through them again:

• Orchestration Server: Acts as a relay and persistent storage for the game.
• Browser: The frontend for the game, where users connect with their wallet and submit a guess. It communicates with the Orchestration Server via HTTP requests.
• MPC-Network: A network of MPC (Multi-Party Computation) servers used to compute coSNARKs¹.
• Smart Contract: A contract on the Optimism mainnet that stores the game's current state and the prize pool.

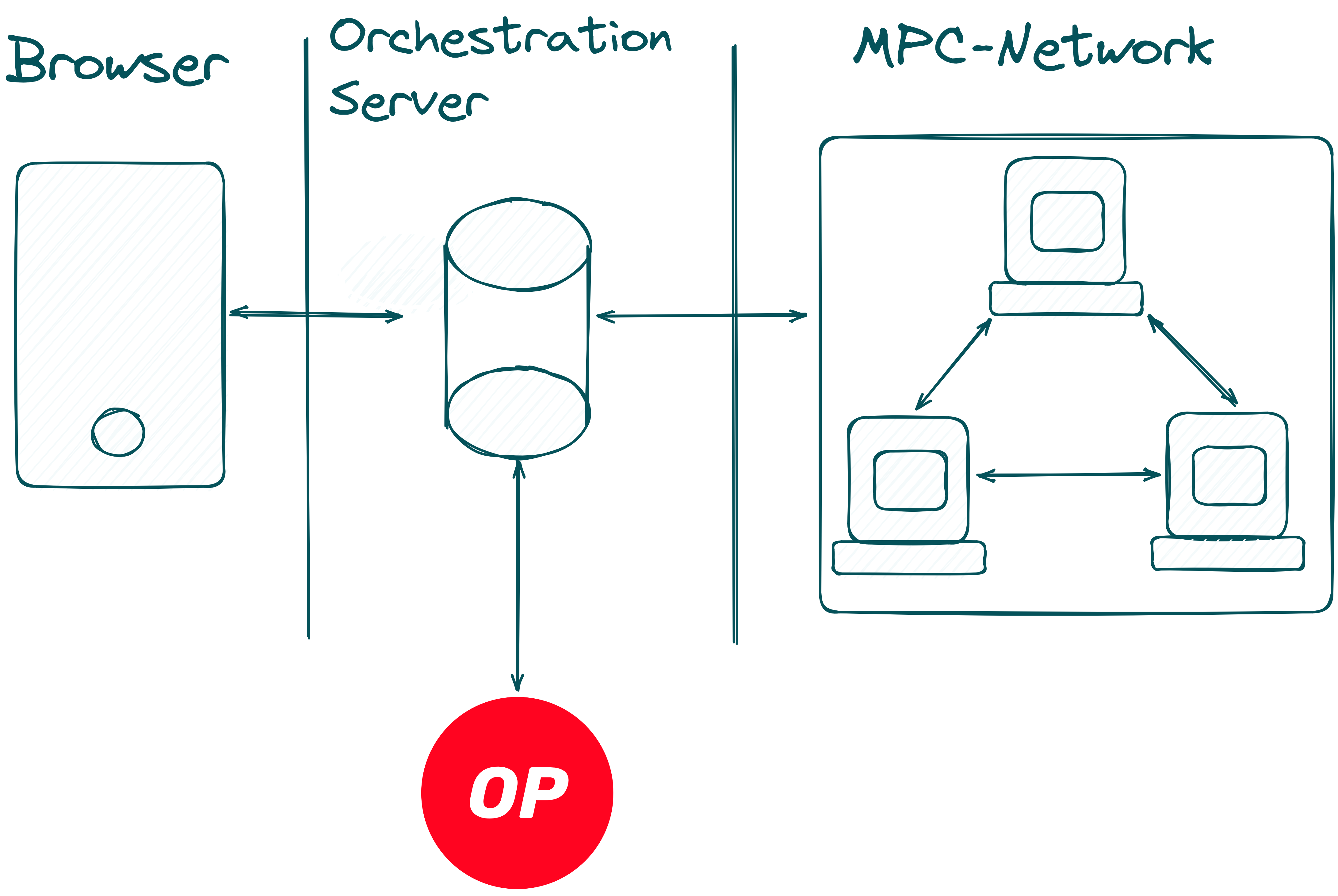
In the upcoming sections, we'll explain what happens when you submit a guess, covering the process from the Browser to the Smart Contract.

Browser

The journey of your guess starts in your Browser. First, you connect your wallet to the game, input your guess $y$, sign "the message" (we'll get to that in a minute), and then submit it. Under the hood, the Browser does a few more things.

First, it samples some randomness $r$ from your operating system. It then secret shares $y$ and $r$ using a 3-party additive replicated secret-sharing protocol² obtaining $\llbracket y\rrbracket $ and $\llbracket r\rrbracket$ which denote the secret shared values of $y$ and $r$. Before we can send $\llbracket y\rrbracket $ and $\llbracket r\rrbracket$ to the Orchestration Server, we need one additional step. Simply sending all shares of $\llbracket y\rrbracket $ and $\llbracket r\rrbracket$ would allow the Orchestration Server to reconstruct the secret values.

Therefore, we encrypt the shares using a public-key encryption scheme with the public keys of the computing nodes of the MPC-Network. This way, only the computing nodes can decrypt their respective shares. The Browser serializes the encrypted shares and base64 encodes them. This base64 encoded string is then signed by your private key from your connected wallet. The Browser sends the signed, base64-encoded string to the Orchestration Server.

Relay at the Orchestration Server

The Orchestration Server receives the signed, base64-encoded string from the Browser and performs some sanity checks:

• It validates the signature using your public key.
• It verifies if you have more than 1$ at mainnet (basic form of bot protection).
• It checks if you have already submitted a guess to prevent multiple submissions.
• It ensures that the maximum number of guesses has not been exceeded.
• Lastly, it checks if guessing-time is up

If all checks pass, the Orchestration Server forwards the shares to the respective nodes in the MPC-Network.

Computing the Commitment to the Guess

Zooming into the MPC-Network, each node receives its respective shares $y_i$ and $r_i$, where $i$ denotes the party, and $y_i$ is the $i$-th share of $y$.

The nodes decrypt the shares and start to compute a coSNARK, which generates a commitment to the values $y$, $r$ and your address. This commitment is a simple Poseidon hash of $y$, $r$ and your address. Additionally, the proof verifies that $y$ is indeed in the range $[1, 1000]$. Remember, the range check is only doable inside the coSNARK, as the value $y$ never left your Browser - only the encrypted shares did.

The computed proof is then sent to the Orchestration Server.

Push the Guess On-Chain

The Orchestration Server receives the proof from the MPC-Network and stores the encrypted shares, the produced commitment, and your address in a database. Remember, the shares are encrypted, so it's impossible for the Orchestration Server—or anyone else, including us—to know the values $y$ and $r$. You'll see later why we need the commitment and the encrypted shares.

The Orchestration Server then sends the proof, attesting that your guess $y$ is indeed between 1 and 1000, along with the commitment, and your address, to the Smart Contract deployed on Optimism. You can check it out on Etherscan ;)

Before storing the commitment in its public state, the Smart Contract performs several checks to ensure the integrity and validity of the submission. Firstly, it repeats some of the checks already done by the Orchestration Server, such as verifying that the maximum number of guesses has not been exceeded and ensuring that you did not already submit a guess. Additionally, the contract verifies that the sender address matches the address of the Orchestration Server, preventing unauthorized submissions.

Obviously, the most important step is verifying the proof. If the proof verifies correctly and the commitment is valid, the contract stores the commitment and the your address in its state. This allows you to easily verify that your guess have been recorded by the contract!³.

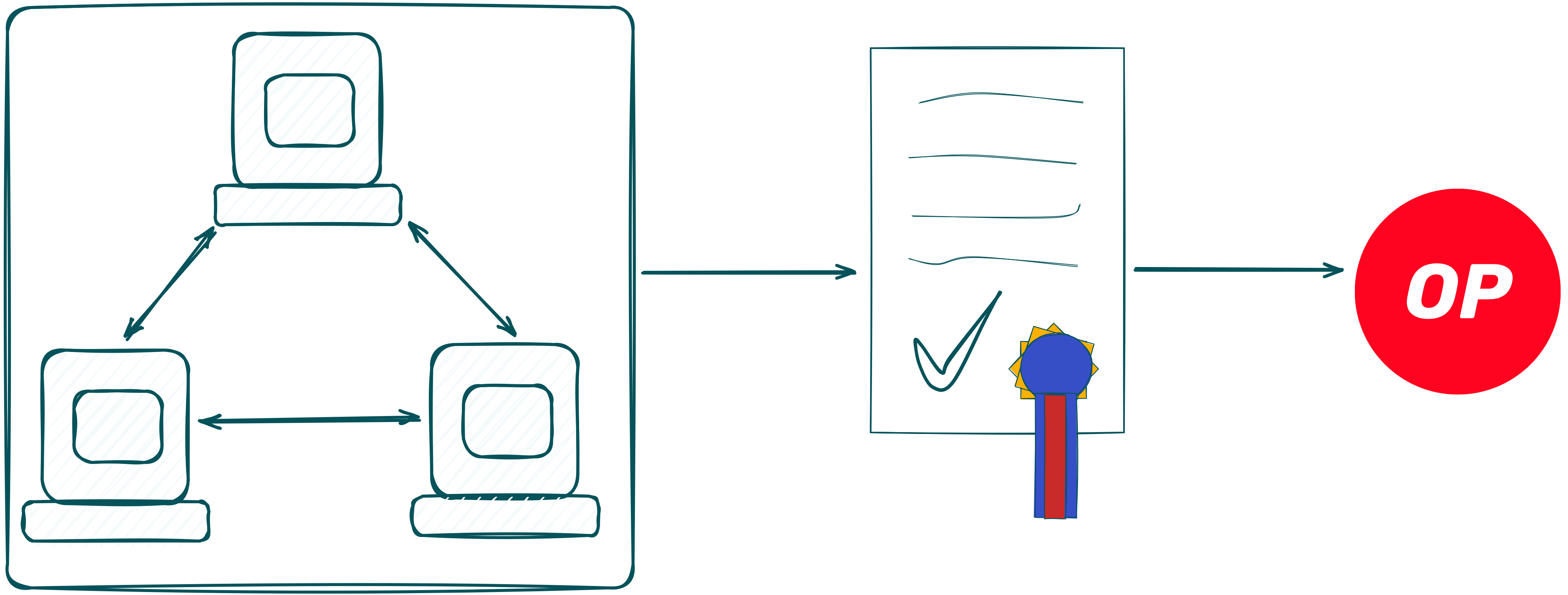
That’s it—the journey of your guess through the system. To summarize:

1. Choose your guess $y$.
2. Sample randomness $r$, secret share $y$ and $r$ and encrypt $\llbracket y\rrbracket $ and $\llbracket r\rrbracket $.
3. Sign the encrypted shares and send them to the Orchestration Server.
4. Perform sanity checks.
5. Compute the commitment to $y$ and $r$ in the MPC-Network and check that $y \in [1,1000]$.
6. Send the proof to the Smart Contract and store the commitment and your address on-chain.

How to Find the Winner

When we deployed the Smart Contract, we set the end game time (the deadline for submitting guesses) to July 15th, 2024, 00:00 UTC. After this time, no more guesses were accepted. Now we needed to find the winner. In the upcoming sections, we'll explain how we did this.

Designing the Winner Circuit

Finding the highest unique guess inside a coSNARK is not as trivial as it might seem, especially in a privacy-preserving way while ensuring soundness. Our primary concern was to prove that we actually used all submitted guesses.

We faced inherent challenges working in an MPC and ZK setting. Both MPC and ZK enforce constant-time algorithms, so traditional sorting algorithms like quicksort or mergesort were off the table. Since we were creating a Groth16 proof with a per-circuit setup, we needed a fixed number of inputs (the circuit would differ for 100 or 1000 guesses). This required padding all guesses to a fixed length and then sorting them. Working with secret-shared values also forces us to use an oblivious sorting algorithm, which ensures we do not learn the order of the submitted values. In summary, we needed an oblivious, constant-time sorting algorithm with a fixed length of 1000.

Our initial design was to provide the 1000 addresses and commitments (including the padded guesses) as public input to the coSNARK, allowing everyone to verify that we used all guesses. However, this approach was not feasible because the auto-generated Solidity verifier obtained by snarkJS exceeded the EVM's size limitations by a (large 😅) margin. For every public input, we need a constant in the verifier contract, resulting in 2000 constants embedded in the contract.

We had to get back to the drawing board, but we came up with another solution, using (once again) our favorite hash function Poseidon!

A Chain of Poseidon Hashes

Instead of providing all 1000 commitments (and addresses) as public input, we chose to hash them in a chain of Poseidon hashes and use the resulting hash as public input. This approach allowed us to prove that we used all guesses without exceeding the EVM's size limitations due to public inputs.

Now, we had a circuit that took the 1000 guesses and randomnesses as private inputs. The Poseidon hash chain, along with the winner's address and the winning guess, served as public outputs (equivalent to public inputs in the verifier's perspective). These three public input constants comfortably fit within the byte limitations of the EVM!

With this problem out of the way, we still had one puzzle piece left: how to actually find the winner in constant time from a sorted list. The same limitations applied here: we needed a constant-time algorithm set to 1000 guesses. Traversing the list of sorted guesses (with the highest at the top), we compared every element with its predecessor, resulting in a vector where the $i$-th element is 1 if the guess is unique and 0 otherwise. Iterating over this vector again, we used multiplexers to find the first element that is 1, identifying the winner. This way, we could maintain constant-time execution.

So, to sum things up, the circuit performs the following steps:

1. Recompute the commitments $a_i = H(y_i, r_i, \text{address}_i)$, where $i$ denotes the $i$-th guess (up to 1000).
2. Compute the Poseidon hash chain $c$ of all commitments such that $c_{i+1} = H(c_i, a_i)$ and $c = c_{1000}$ and $c_0 = 0$.
3. Sort the secret-shared guesses (and associated address) with a constant-time oblivious sorting algorithm⁴.
4. Find the highest unique guess in the sorted list as described above.
5. Set the winner's address, the winning guess, and $c$ as outputs (which are public inputs from the verifier's POV).

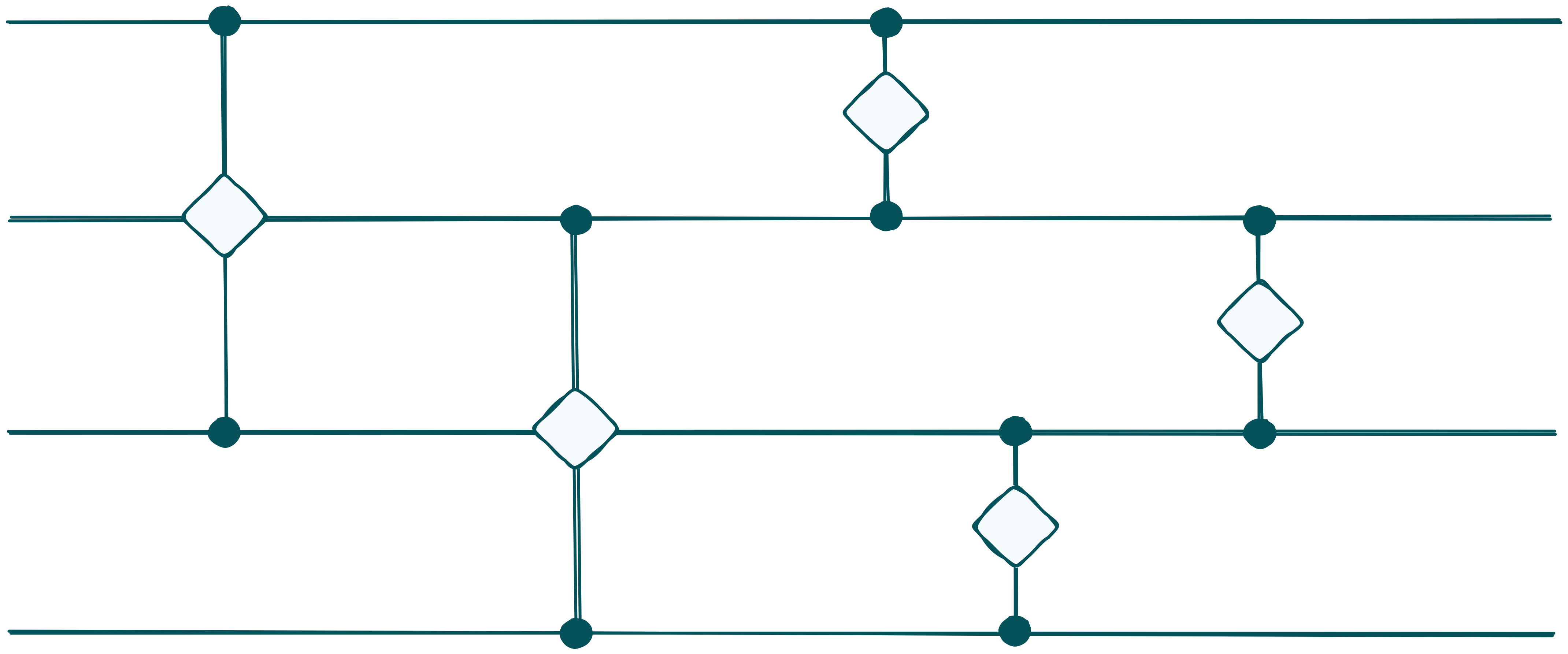
Sorting networks are constant-time algorithms

We now have our winner circuit in place. The next step is to tell the Smart Contract that the game is over and that it should cash out the winner.

Finding the winner

After the game's end time, the Orchestration Server triggers the MPC-Network by sending the (padded) set of guesses to the nodes. The nodes then execute the winner circuit, yielding the winner's address, the winning guess, and the Poseidon hash chain $c$.

We submit the winner's address and the winning guess to the Smart Contract, omitting $c$. The Smart Contract recomputes $c$ from its public state. This way, if you checked that your commitment is in the public state of the Smart Contract, you can be sure that your guess was considered when the MPC-Network determined the winner.

The verifier contract expects three public inputs to check the submitted proof: the winner's address, the winning guess, and $c$ from the Smart Contract. We verify the proof with these three inputs. If the proof verifies, the winner receives their payout! Which in our case was $994 for 0x381f35f3817eee7eee571e5002db13c66e69971f. Congratulations! 🎉

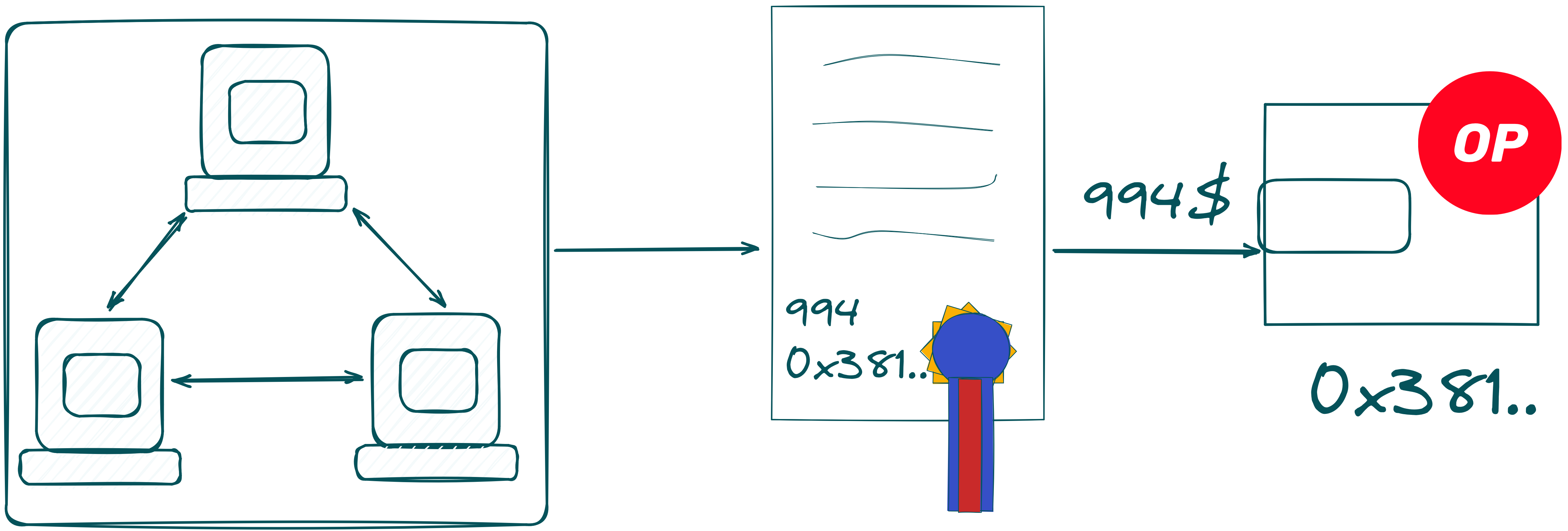
Some Insights

With the technical talk behind us, we'd like to share some insights we gained during the development of the Max Pick Challenge. First and foremost, we realized (or more accurately, confirmed) that we are not web developers 😅. We spent a lot of unexpected time on the frontend, experimenting with various ideas.

Additionally, we encountered a rather painful issue of alloy-rs. This problem surfaced for the first time during our live run and never appeared during testing. We had to quickly implement a band-aid fix without losing the already submitted guesses, which we thankfully managed to do!

On a brighter note, building an end-to-end demo, from frontend to Smart Contract, was a great test for our tooling. We found and fixed some bugs during the process and identified several quality-of-life improvements needed for our tools. One interesting challenge was that we didn't have an efficient way to retrieve the output of a circuit. We had to manually extract the value from the shared witness, which highlighted a significant area for improvement.

What's Next?

So, what’s next for coCircom? As we mentioned, we learned a lot about our tooling, especially coCircom, and not everything we wanted to improve was doable in the short timeframe we had for the demo (2 weeks from idea to EthCC, where we launched the game). This means we have some tasks to tackle in the near future:

1. Improve the Speed of the Witness Extension
   • The most interesting insight we gained is that the witness extension is the bottleneck of our tooling.
   • Initially, we started with 100 guesses using a simple insertion sort algorithm. When we scaled up to 1000 guesses, our server ran into memory constraints and killed the witness extension process.
   • Even with all improvements we could think of, the witness extension still takes about an hour for 1000 guesses, highlighting the necessity for improvement.
2. Support PLONK
   • Currently, we only support Groth16, but we plan to support PLONK as well. This may or may not impact the speed of the witness extension.
3. Research and Implementation of Modern ZK Proof System improvements
   • Supporting modern improvements for ZK proof systems, especially lookup tables, requires additional research. Efficiently supporting these improvements is a longer-term goal.

Conclusion

So, that's a wrap! Thanks again to all participants and congratulations to the winner! As promised, we donated the rest of the prize pool to the ZK Podcast Team. As the winning guess was quite high, the donation amount wasn't much, but still, we stand to our word 😉.

We hope you enjoyed the challenge and maybe learned something new about coSNARKs and MPC. If you have any questions or feedback, feel free to reach out to us on X (Twitter) or join our Discord. We're always happy to chat!

Until next time, happy hacking! 🚀